Расположение - терм
Cтраница 1
 |
Расщепление термов основного состояния ионов от Ti3 до Си2 в октаэд-рическом поле. Цифра в скобках - степень вырождения уровня. [1] |
Расположение термов симметрично относительно 5-терма d5 - конфигурации. [2]
 |
Расщепление термов основного состояния ионов от Ti34 до Си2 в октаэдрическом поле. Цифры в скобках - степень вырождения уровня. [3] |
Расположение термов симметрично относительно S-терма - конфигурации. [4]
 |
Расщепление термов основного состояния ионов от Ti3 до Си2 в октаэд-рическом поле. Цифра в скобках - степень вырождения уровня. [5] |
Расположение термов симметрично относительно 5-терма d5 - конфигурации. [6]
Точно совпадали с опытными данными расположение термов, правила отбора и интенсивности линий. [7]
Таким образом, если при я - 3 расположение термов еще аналогично случаю системы одиночников и триплетов, то при больших п термы попарно группируются около своих пределов. [8]
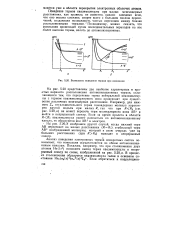 |
Возможное поведение термов при ионизации. [9] |
На рис. 5.20 представлены два наиболее характерных и простых варианта расположения автоионизационных термов, отличающихся тем, что пересечение терма нейтральной квазимолекулы с термом квазимолекулярного иона происходит при существенно различных межъядерных расстояниях. Например, для нижнего 2 отталкивательного терма гомоядерных молекул характерен крутой подъем при малых R, так что при RRo ( см. рис. 5.20, а) он может пересечь терм молекулярного иона АВ и выйти в непрерывный спектр. Если за время пролета в области RRo квазимолекула успеет распасться по автоионизационному каналу, то образуются ион АВ и электрон. [10]
В конце записи каждого факта ставится точка. Расположение термов в предикате упорядочено. [11]
Для данной электронной конфигурации атома могут существовать несколько термов. Порядок расположения термов по энергии определяется эмпирическими правилами Хунда. [12]
Совершенно точные суждения можно извлечь из любых свойств симметрии, которыми должна обладать волновая функция в силу симметрии, присущей соответствующей задаче. Наиболее важное из этих свойств симметрии состоит в полной эквивалентности электронов и следующей отсюда неразличимости их; волновая функция должна быть, конечно, одинаковой в случаях, когда, скажем, первый электрон находится на / С-оболочке, а второй - на L-оболочке и когда, наоборот, второй находится на Х - оболочке, а первый - на L-оболочке. Это ведет к общим правилам расположения термов в атомах с несколькими валентными электронами. [13]
Однако орбита имеет только один период. Эта сумма называется главным квантовым числом, так как именно им определяется расположение термов в невозмущенном движении. [14]
 |
Термы различных конфигураций эквивалентных неэквивалентных электронов. [15] |
Страницы: 1 2