Распределение - источник - тепло
Cтраница 1
Распределение источников тепла определяет поле температур. Поэтому, если Б модели Ачарда стационарное температурное поле вдоль оси луча всегда имеет максимум ка нексч ипой глубине, то темг. [1]
В настоящей работе исследован закон распределения источников тепла по длине цилиндра практически во всем диапазоне частот. Исследование функции проведено в несколько этапов так, чтобы на каждом этапе было минимальное число параметров. [2]
Эту функцию можно рассматривать как плотность распределения источников тепла, выделяющих суммарно единицу количества тепла. [3]
 |
Предельное уменьшение расхода при количественном регулировании типовых воздухораспределителей. [4] |
Коэффициент воздухообмена зависит от способа организации и интенсивности воздухообмена, вида, мощности и распределения источников тепла в помещении. [5]
Когда число парциальных источников конечно или, что всегда имеет место на деле, когда распределение источников тепла достаточно точно описывается конечным числом слагаемых, такая перестановка порядка суммирования возможна. [6]
Так как коэффициенты gt в формулах ( 303) - ( 308) определяются функцией распределения источников тепла в плите, мож - ЛО. & определять мшцносн нагрооатоль - ных элементов в соответствии с конкретными требованиями, предъявляемыми к рельефу температурного поля и скорости прогрева ( охлаждения) плиты. [7]
Следует подчеркнуть, что стенки каналов ( их размеры, конфигурация, теплофизические свойства, интенсивность и распределение источников тепла) могут влиять на теплообмен с потоком, непосредственно воздействуя только на граничные условия. [8]
При выборе расчетных схем следует учитывать принцип местного влияния, который показывает, что температурное поле зависит от размеров и характера распределения источника тепла только на расстояниях одного порядка с его размерами; на больших расстояниях температурное поле практически не зависит от формы источника и занимаемого им объема. [9]
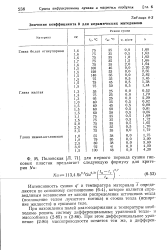 |
Значение коэффициента Ь для керамических материалов. [10] |
Интенсивность сушки q и температура материала t определяются по основному соотношению ( 6 - 4), которое является справедливым независимо от закона распределения источников тепла ( поглощение телом лучистого иотока) и стоков тепла ( испарение жидкости) IB сушимом теле. [11]
Вообще при выборе расчетных схем следует учитывать принцип местного влияния, который утверждает, что температурное поле существенно зависит от размеров и характера распределения источника тепла только на расстояниях одного порядка с его размерами, тогда как на больших расстояниях температурное поле практически не зависит от формы источника и занимаемого им объема. [12]
В [1] описаны результаты большого количества численных экспериментов по моделированию конвекции в верхней мантии, выполненных в двумерном приближении при разных значениях скорости выделения тепла и при различных типах распределений источников тепла: внутри слоя, частично внутри, а частично при задании потока тепла на нижней границе и при задании всего потока тепла только снизу. [13]
В том случае, когда следующий импульс накачки производится до того, как успеет произойти выравнивание ( релаксация) температуры, после окончания этого импульса температурное поле будет определяться суперпозицией составляющих, отвечающих распределению источников тепла и релаксационному температурному полю. При поступлении последующих импульсов накачки относительный вклад релаксационного поля в результирующее температурное распределение становится все большим и установившийся профиль температуры весьма сильно отличается от распределения источников тепла, а температурные перепады значительно превосходят те, которые обусловлены лишь неравномерностью накачки в режиме одиночных вспышек. После выхода на квазистационарный режим в каждом последующем импульсе температурное поле воспроизводится. [14]
С ( z - коэффициент теплоемкости среды в Дж / ( м К); A ( z) - коэффициент теплопроводности среды, Вт / ( м - К); / ( z) - плотность распределения источников тепла. [15]
Страницы: 1 2