Распределение - концентрация - вещество
Cтраница 3
Массоотдача при адсорбции из растворов есть процесс переноса вещества в направлении поверхности частицы, связанный с неравномерностью распределения концентрации вещества в слое жидкости, прилегающем к поверхности твердого тела. [31]
Такой прием замены реального процесса, протекающего непрерывно, многоступенчатым, дискретным позволяет сравнительно легко вывести уравнение, отражающее распределение концентрации вещества в слое адсорбента. Подобное уравнение было получено из теории скоростей [ см. уравнение (1.11) ], что позволяет связать обе теории между собой. [32]
Представляется целесообразным найти простую приближенную формулу для расчета приземной концентрации вредного вещества при выбросе из труб, описывающую основные закономерности распределения концентрации вещества. [33]
Таким образом, для того чтобы решить гидродинамическую задачу о движении жидкости с учетом изменения S на межфазной поверхности, необходимо предварительно знать распределение концентрации вещества, температуры и заряда на поверхности. Их распределение, в свою очередь, связано с распределением гидродинамических параметров. Таким образом, решение этой задачи требует привлечения уравнений сохранения массы, количества движения, энергии и заряда с соответствующими граничными условиями, отражающими баланс сил на межфазной поверхности: равенство тангенциальных сил и скачок нормальных сил, равный капиллярному давлению, а в случае модели Буссинеска - учет поверхностной вязкости слоя. [34]
Описанный прием замены реального процесса, протекающего непрерывно, многоступенчатым позволяет сравнительно легко вывести уравнение, выражающее форму размывания зоны и, следовательно, распределения концентрации вещества в слое сорбента. Подобное уравнение было нами получено и из теории скоростей, что позволяет связать обе теории между собой. [35]
Переходя к рассмотрению расчета адсорбционных установок с кипящим слоем непрерывного действия, отметим, что при организации непрерывного процесса по высоте слоя устанавливается стационарный профиль кривой распределения концентрации вещества в газовом потоке. [36]
Ввиду незначительных размеров зон [ 0; а ( т) ], [ 0; ( т) ], [ ( т); d ( OL а также с целью упрощения, представим законы распределения концентраций веществ ( агрессивной среды и Са ( ОН) 2) в них линейными. [37]
В данном случае естественно задаться распределением концентрации А, так как потребление А происходит только в одной реакции со значительной теплотой активации и, следовательно, доходит практически до конца в узкой зоне реакции разветвления. Распределение концентрации вещества А вне зоны химической реакции разветвления при х 0 является экспоненциальным. Потребление А сопровождается одновременным образованием В в реакции разветвления. Вне узкой зоны реакции разветвления В только расходуется в реакции рекомбинации. Следовательно, в зоне разветвления концентрация В имеет максимум, величина которого зависит от скорости рекомбинации. [38]
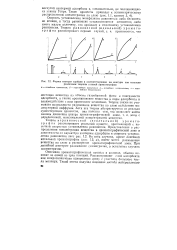 |
Формы изотерм сорбции и соответствующие им контуры зон согласно различным теориям газовой хроматографии. [39] |
Теория неравновесной ( неидеальной) хроматографии рассматривает реальный процесс, протекающий с конечной скоростью установления равновесия. Представление о распределении концентрации вещества в хроматографической зоне в зависимости от характера изотермы адсорбции и скорости установления равновесия дает рис. 1.2. Во всех случаях, кроме линейной идеальной хроматографии ( рис. 1.2, а), имеет место размывание вещества по слою и расширение хроматографической зоны. При линейной изотерме размывание симметрично, в остальных случаях асимметрично. [40]
Несколько краевых задач в неподвижной среде будут рассмотрены ниже в связи с их физико-химическими приложениями, а также для сравнения решений диффузионной задачи в неподвижной и движущейся среде. В некоторых случаях приходится изучать распределение концентрации вещества, которое изменяется в результате химических или иных процессов, например в результате рекомбинации или ионизации, происходящих во всем объеме жидкости, или некоторой объемной химической реакции, в которой участвуют растворенные частицы. Пусть в некотором элементе dVt находящемся в объеме жидкости, возникает или исчезает вещество. Обозначим через Q0 ( r) dV число частиц, возникающих в 1 сек в объеме dV, находящемся вокруг точки г. Величина Q0 носит название мощности источника. Если частицы исчезают, а не возникают, то Q0 отрицательно. [41]
 |
Типичная выходная кривая прояви-тельного метода. [42] |
На выходе вещества из колонки вследствие его десорбции зона расширяется в Го раз, а максимальная концентрация уменьшается в это же число раз. Таким образом, после вымывания распределение концентрации вещества не отличается от его распределения в слое по форме и отличается только масштабом. [43]
На выходе вещества из колонки вследствие его десорбции зона расширяется в Г0 раз, а максимальная концентрация уменьшается в Г0 раз. Таким образом, после вымывания распределение концентрации вещества не отличается от его распределения в слое по форме и отличается только масштабом. [44]
Электролиз вызывает изменение ряда свойств электрохимической системы: с течением времени меняются количества компонентов в фазах системы, нарушается гомогенность распределения концентраций веществ, в некоторых случаях возникают новые фазы. Электролиз возможен, когда напряжение на электродах больше ЭДС элемента, в котором равновесно протекает химическая реакция, обратная электролизу. [45]
Страницы: 1 2 3 4