Распределение - упругое напряжение
Cтраница 1
Распределение упругих напряжений в анизотропной пластине с трещиной, полученное независимо в работах [28, 38], можно найти при помощи метода комплексных переменных. Впоследствии было показано [72], что для любого произвольного плоского нагружения распределение напряжений можно разделить на симметричную и антисимметричную компоненты и таким же образом проделать общую процедуру определения коэффициентов интенсивности напряжений. [1]
Распределение упругих напряжений вокруг скважины. [2]
Картины распределения упругих напряжений, получаемые оптическим методом на прозрачных веществах, справедливы и для непрозрачных однородных материалов. При резании инструмент находится в упругом напряженном состоянии. Применяя в качестве резца прозрачный материал, оптическим методом можно определить напряжения в теле резца и на его поверхности. [3]
Характер распределения упругих напряжений в зонах возможного разрушения определяем по результатам испытания плоской модели телескопического кольца ( рис. 3.8, а) из оптически активного материала на поляризационно-оптической установке. Плоская модель позволяет достаточно точно воспроизвести НДС в зонах разрушения на концевых участках полукольца. При испытании модели из оптически активного материала имитировали перекос при эксплуатации элементов телескопического соединения путем изменения расстояния JC от точки приложения силы Р до внутренней цилиндрической поверхности кольца и варьировали радиусы R А и R B опасных зон исследуемой детали. [4]
Характер распределения упругих напряжений в зонах возможного разрушения определяем по результатам испытания плоской модели телескопического кольца ( рис. 3.8, а) из оптически активного материала на поляризационно-оптической установке. Плоская модель позволяет достаточно точно воспроизвести НДС в зонах разрушения на концевых участках полукольца. При испытании модели из оптически активного материала имитировали перекос при эксплуатации элементов телескопического соединения путем изменения расстояния х от точки приложения силы Р до внутренней цилиндрической поверхности кольца и варьировали радиусы R А и R B опасных зон исследуемой детали. [5]
Естественные напряжения и давления в горных породах, распределение упругих напряжений вокруг скважины. [6]
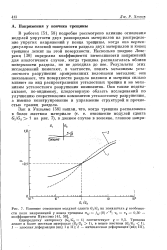 |
Влияние отношения модулей сдвига GtIG2 на показатель g особенности поля напряжений у конца трещины - ftj ( в r - 8. v1 - v2 0 30 - коэффициенты Пуассона. [7] |
В работах [51, 58] подробно рассмотрено влияние отношения модулей упругости двух разнородных материалов на распределение упругих напряжений у конца трещины, когда она перпендикулярна плоской поверхности раздела двух материалов и конец трещины лежит на этой поверхности. Несколько позднее Леве-ренц [38] определил коэффициенты интенсивности напряжений для аналогичного случая, когда трещина располагалась вблизи поверхности раздела, но не доходила до нее. Результаты этих исследований помогают, в частности, понять механизмы усталостного разрушения армированных волокнами металлов; они показывают, что поверхности раздела волокон и матрицы сильно влияют на вид распространения усталостных трещин и на механизмы усталостного разрушения композитов. Они также подсказывают, по-видимому, плодотворную область исследований по улучшению сопротивления композитов усталостному разрушению, а именно конструирование и управление структурой и прочностью границ раздела. [8]
Прежде чем перейти к рассмотрению следующего случая, следует вспомнить очень важное обобщение, касающееся влияния определенного типа нагрузок на распределение упругих напряжений, которые являются очень полезными при оценке порядка ошибки, которая вносится при некоторых определенного вида упрощениях. Принцип Сен-Венана, - сформулированный известным ученым и инженером, жившим в девятнадцатом веке, утверждает, что если система цагрузок, приложенная на малой области упругого тела, заменяется статически эквивалентной аналогично приложенной системой, то влияние возникающих в теле напряжений будет носить локальный характер, становясь пренебрежимо малым уже на расстояниях от области приложения, сопоставимых с размером этой области; отсюда следует, что если система нагрузок является самоуравновешенной, то ее можно заменить нулем и тем самым она может быть либо снята, либо приложена, вызывая при этом только локальные изменения распределения напряжений. [9]
Сравнительные испытания, проведенные на металлических структурах, снабженных датчиками напряжений, и на замороженных фотоупругих моделях, показали, что при осторожной шлифовке или разрезании моделей на части напряжения в них не изменяются и что картина напряжений, наблюдаемая на фотоупругой модели, очень хорошо согласуется с распределением упругих напряжений в металлическом оригинале. [10]
Тем не менее этот метод дал первое упруго-пластическое ( в противоположность жестко-пластическому, см. гл. Распределение упругих напряжений описывается бигармоническим уравнением. [11]
Тем не менее этот метод дал первое упруго-пластическое ( в противоположность жестко - пластическому, см. гл. Распределение упругих напряжений описывается бигармоническим уравнением. [12]
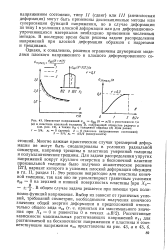 |
Изменение напряжений а o gg О я / 2 с расстоянием г / а ( а в пластине конечной толщины В, содержащей отверстие радиуса а. [13] |
Многие важные практические случаи трехмерной деформации не могут быть смоделированы в условиях радиальной симметрии, например трещины в пластинах умеренной толщины и полуэллиптические трещины. Для задачи распределения упругих напряжений вокруг круглого отверстия в бесконечной пластине произвольной толщины было получено аналитическое решение [27], вариант которого в условиях плоской деформации обсужден в гл. [14]
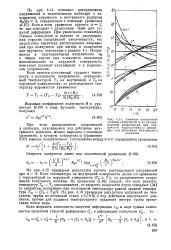 |
Влияние показателя степени. ползучести а на распределение напряжений при ползучести толстостенного цилиндра под действием внутреннего, давления. [15] |
Страницы: 1 2