Распределение - контактное напряжение
Cтраница 1
Распределение контактных напряжений в значительно мере зависит от принятой расчетной модели сооружения. В настоящее время в основном используют две модели: модель недеформируемого сооружения ( часто говорят совершенно жесткого сооружения) и модель сооружения конечной жесткости. [1]
Изучается распределение контактных напряжений, а также расположение зон сцепления и проскальзывания в области контакта в зависимости от формы индентора и действующих на него сил и моментов. [2]
Исследовано распределение контактных напряжений. Показано, что вблизи неугловых точек границ штампа поле напряжения имеет классическую корневую особенность, а в окрестности вершин штампа - слабую степенную особенность с вещественным показателем. Подробно изучена зависимость показателя особенности от угла раствора границ штампа. Получены интегральные представления для коэффициентов интенсивности напряжений на ребрах штампа. [3]
Изучается распределение контактных напряжений, а также расположение зон сцепления и проскальзывания в области контакта в зависимости от формы индентора и действующих на него сил и моментов. [4]
Закон распределения контактных напряжений при симметричном расположении полости практически не искажается. Изменяется только амплитуда контактных напряжений, что соответствует изменению АЧХ штампа. При асимметричном расположении полости относительно штампа, например, при анализе плоской задачи, положение полости определяет степень асимметрии в законе распределения контактных напряжений наряду с количественным изменением амплитуды. [5]
По теории Герца распределение контактных напряжений и зона проскальзывания А ( рис. 2) в упругом верхнем диске будут иметь те же значения, что получаются при замене диска упругой верхней полуплоскостью. [6]
Требуется определить закон распределения контактных напряжений q ( t, x) на линии соединения стрингера с полуплоскостью. При этом, как обычно [151, 610], предполагается, что стрингер лишен изгибной жесткости и находится в одноосном напряженном состоянии. [7]
Требуется определить закон распределения контактных напряжений в полоске соединения накладки с полупространством, когда она загружена указанными на рисунке силами. [8]
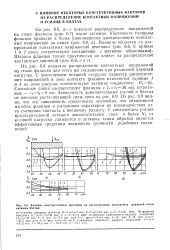 |
Влияние конструктивных факторов на распределение контактных давлений после затяжки болтов. [9] |
На рис. 6.8 показано распределение контактных напряжений на стыке фланцев для этого же соединения при различной внешней нагрузке. Сплошные линии соответствуют фланцам с t t2 3Q мм, штриховые - / 1 / 2 9 мм. Зависимость дополнительных усилий в болтах от внешней растягивающей силы дана на рис. 6.9. Из рис. 6.9 видно, что эта зависимость существенно нелинейна, что объясняется изгибом фланцев и рычажным характером их взаимодействия из-за смещения контакта к внешнему радиусу. С увеличением усилия предварительной затяжки дополнительная сила в болте Л от внешней нагрузки снижается и затяжка таким образом является эффективным средством повышения прочности резьбовых соединений. [10]
В работе [6] рассмотрено распределение контактных напряжений при осадке свинцовых и алюминиевых образцов с применением универсального штифта. [11]
В работе [31] исследовано распределение контактных напряжений методом наклонных точечных месдоз при волочении стальных ( Ст 3) прутков и труб. [12]
В работах [78, 79] изучали распределение контактных напряжений вдоль стенки контейнера при прямом и обратном прессовании свинцовых полос и прутков, а также при закрытой прошивке с образованием стакана. [13]
На рис. 12 показано распределение безразмерных контактных напряжений ( т / Е под штампом при следующих безразмерных прижимных усилиях УДЯ Я): 1) 6.6 КГ7, 2) 4.86 1 ( Г5, 3) 5.5 ИГ8, а на рис. 13 изображена зависимость краевой нагрузки от интервала контакта. [14]
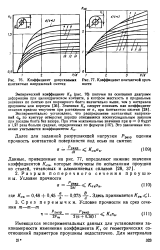 |
Коэффициент допускаемых контактных иаприжений смятии.| Коэффициент контактной прочности. [15] |
Страницы: 1 2 3 4