Распределение - паскаль
Cтраница 2
Представление F ( т) в виде функции бета-распределения позволяет естественным образом определить F ( т) при всех действительных неположительных значениях параметра г. В таком расширенном толковании распределение Паскаля называют отрицательным биномиальным распределением. [16]
Но вот что интересно: какую бы модель мы ни взяли и какие бы вероятностные распределения ни применяли, нам всегда удастся получить стоимостную оценку, соответствующую текущему состоянию рынка, если будем выяснять подразумеваемую волатильность на основании последних рыночных котировок. А в модели, прибегающей к распределению Паскаля, - менять период или вводить предположения относительно будущей величины среднего абсолютного изменения цены, попутно включая поправки для хвостов, а также растущего и снижающегося рынка. Можно попытаться выяснить стоимость опциона с помощью биномиальной модели, но в нее все равно придется вводить предположения о величине вероятного изменения цен. Таким образом, какая бы модель ни использовалась, нам всегда приходится выдвигать предположения относительно волатильности, которую мы пытаемся выяснить тем или иным образом, введя ее потом в какую-либо модель. [17]
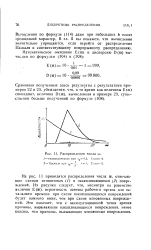 |
Распределения числа ш. [18] |
II мы покажем, что вычисления значительно упрощаются, если перейти от распределения Паскаля к соответствующему непрерывному распределению. [19]
Паскаля, мы получим более высокие стоимостные оценки опционов вне денег по сравнению с моделью Блэка - Шоулза или Блэка. В зависимости от степени расхождения между историческими и ожидаемыми оценками в отношении волатильности, стоимость опциона у денег может оказаться одинаковой, либо дать более высокую оценку для распределения Паскаля. [20]
Общепринятые модели ценообразования опционов имеют и другие проблемы. Так, остается открытым вопрос о практичности использования логнормального вероятностного распределения цен. На фондовом рынке такой подход еще оправдан, но при работе с процентными инструментами, где с успехом применяется распределение Паскаля, он оказывается под большим сомнением. Неоднозначно также можно относиться к использованию в моделях срока до истечения опционов, выражаемого как часть года. В ряде случаев представляется практичным использовать не 365-дневную базу для расчетов доли года, а ориентироваться на число торговых дней в году. Определенное беспокойство по поводу точности существует даже в отношении исторической волатильности, о чем свидетельствуют многочисленные варианты ее исчисления. [21]
В нашей задаче о времени ожидания г обязательно является положительным целым, но величина, определяемая либо (8.1), либо (8.2), неотрицательна и (8.3) справедливо для любого положительного г. Для произвольных фиксированных О0 и 0р1 последовательность / ( &; г, р называется отрицательным биномиальным распределением. Оно встречается во многих приложениях ( и мы уже сталкивались с ним в задаче 24 гл. Для положительных целых г последовательность / ( &; г, р) можно интерпретировать как вероятностное распределение времени ожидания r - го успеха; в такой форме оно также называется распределением Паскаля. [22]
Для произвольного, но фиксированного действительного числа г О и 0р 1 последовательность / ( k; r, р) определяет отрицательное биномиальное распределение. Оно встречается во многих приложениях ( мы сталкивались с ним в задаче 24 гл. Если г - целое, то / ( ft; r, р) можно интерпретировать как распределение вероятностей времени ожидания r - го успеха; в такой форме оно также называется распределением Паскаля. [23]
Страницы: 1 2