Распределение - спиновая плотность
Cтраница 3
Из экспериментальных констант СТС найдено распределение спиновой плотности по молекуле. [31]
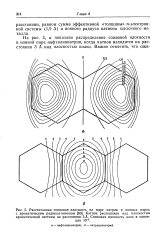
На рис. 5, а показано распределение спиновой плотности в ионной паре нафталиннатрия, когда катион находится на расстоянии 3 А над плоскостью колец. [33]
В настоящее время существует возможность оценки распределения спиновой плотности в а-радикалах на основе теории молекулярных орбиталей ( с учетом атомных орбиталей всех валентных оболочек), как это делается, например, в методе INDO, упомянутом в разд. [34]
Анализ констант анизотропного СТВ показывает, что распределение л-электронной спиновой плотности в ДФПГ в твердых матрицах по сравнению с распределением в ДФПГ в растворах мало изменяется. Этот вывод следует также из того, что а и Q для радикала в жидкости и стеклах отличаются незначительно. Различия изотропных констант аУ и спин-поляризационных параметров Q для радикала в растворах и стеклах, по мнению авторов работ [16, 31], вызваны искажением вблизи р-атома азота геометрии радикала в твердой матрице. [35]
На рис. 5, б показана карта распределения спиновой плотности для ионной пары антраценнатрия. В этом случае максимальная спиновая плотность должна быть на катионе, расположенном над центром молекулы, причем это положение энергетически также предпочтительно. Снова порядок рассчитанных спиновых плотностей хорошо согласуется с опытными данными. [36]
Сравнение результатов расчета с экспериментом показывает, что распределение спиновой плотности в этиле хорошо описывается по методу Мак-Лечлана, особенно если учесть изменение орбитали неспаренного электрона. [37]
Таким образом, пока что все результаты изучения распределения спиновой плотности методом ЭПР соответствуют предсказаниям, сделанным на основе простого применения концепции электроотрицательности к радикалам, имеющим одинаковое геометрическое строение. [38]
Заместители в пара-положении фенильных колец вызывают небольшое изменение распределения спиновой плотности в радикале. [39]
Расчет по модели sp - гибридизации приводит к распределению спиновой плотности, при котором 4 группы протонов - орто -, пара -, лета-протоны фенильных колец и лета-протоны пикриль-ного кольца эквивалентны. Такое распределение спиновой плотности полностью соответствует экспериментальным константам СТВ с протонами в радикале, в то время как результаты расчетов по модели 5р2 - гибридизации плохо согласуются с экспериментом: согласно расчету должно быть почти в два раза большее число групп эквивалентных протонов. [40]
Это позволяет определить влияние включения второго бензольного кольца на распределение спиновых плотностей, сопоставляя спектры ЭПР замещенных нитро-дифенилов и соответствующих бензолов. [41]
Однако результаты этих расчетов неоднозначны и противоречивы, так как распределение спиновой плотности весьма чувствительно к выбору параметров гетероатомов. [42]
 |
Результаты расчетов триплетного состояния молекулы бутадиена. [43] |
У 4ВС ( с учетом только ковалентных структур) дает очень разумное распределение спиновой плотности, хотя и совершенно нереалистичное значение энергии. [44]
 |
Константы СТВ ( в э в замещенных бензильных радикалах. [45] |
Страницы: 1 2 3 4 5