Распределение - погрешность - размер
Cтраница 1
Распределение погрешностей размеров ( линейных и угловых) заготовок и деталей, погрешностей настройки, расположения заготовок в приспособлениях, значений шероховатости, твердости поверхности и других физико-механических свойств деталей может подчиняться нормальному закону. Нормальный закон распределения является предельным законом, к которому при определенных условиях приближаются многие другие законы. [1]
Законы распределения погрешностей размера и формы зависят от законов распределения исходных факторов и от вида аналитических зависимостей, связывающих постоянные и переменные вдоль координат ф и / производственные погрешности с исходными факторами. [2]
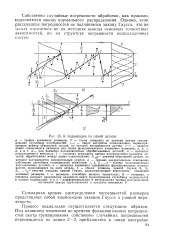 |
К подналадке по одной детали. [3] |
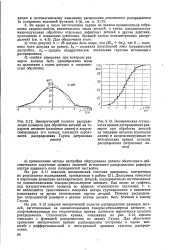
Суммарная кривая распределения погрешностей размеров представляет собой композицию законов Гаусса и равной вероятности. [4]
Суммарная кривая 4 распределения погрешностей размеров представляет собой композицию законов Гаусса и равной вероятности. [5]
В этом случае суммарный закон распределения погрешностей размеров партии деталей получается гауссовым. [6]
Эта формула дает возможность получить не только суммарный закон распределения погрешностей размеров и формы, рассматриваемых в виде случайной функции. Она может быть использована и для упрощенных математических расчетов по суммированию отклонений размеров и формы, представляемых как случайные величины. В последнем случае плотность вероятности суммарной погрешности размеров и формы находятся как композиция законов Гаусса и. Заметим, что в этом случае огранка с нечетным числом граней не учитывается в общей погрешности обработки, так как диаметр детали является постоянным. [7]
Условие ( IV-1) безусловно выполнимо в крупносерийном, массовом и, особенно, автоматизированном производствах, поскольку для таких производств характерно распределение погрешностей размеров деталей, следующее закону нормального распределения. [8]
Наряду с вероятностными характеристиками, являющимися функциями угловой координаты детали, при расчете точности обработки требуется знать, кроме того, суммарный закон распределения погрешности размеров с учетом отклонений формы. [9]
Диаграмма относится к наружным диаметрам цилиндрических деталей, последовательно изготовленных на одношпиндельном токарно-револьверном автомате. Поэтому распределение погрешностей размеров в данном случае должно быть близким к закону Гаусса. [11]
Рассмотрим один из возможных вариантов системы автоматической оптимизации для управления технологическим процессом токарной обработки. Значения параметров v, t и s, при которых достигается этот экстремум, находится в процессе функционирования системы, поэтому автоматический поиск является наиболее характерным признаком автоматической оптимизации. Величина экстремума целевой функции Q и соответствующие ей значения управляющих параметров могут существенно изменяться в зависимости от условий протекания технологического процесса. Однако устройство автоматического поиска находит новое значение экстремума независимо от причин, вызывающих его смещение в процессе работы. Дляг решеяте-задата - упуа & лешге - процессом текарйей-обра ботки деталей подшипников разработаны различные варианты подналадок, проводящихся со случайными ошибками, для элиминирования размерного износа режущего инструмента ( гл. При этом рассчитываются оптимальные параметры подналадок для обеспечения минимума дисперсии распределения погрешностей размеров. В частности, для случая проведения подналадок через фиксированное число деталей найдены формулы для определения оптимального интервала подналадок, зависящего от интенсивности износа и среднего квадратического отклонения ошибок подналадок. [12]
Страницы: 1