Распределение - полюс
Cтраница 3
Очевидно, что полюсы Н ( р), расположенные в правой полуплоскости, могут быть нулями только Pi ( - р), так как N ( p) не может иметь полюсов в правой полуплоскости. Распределение полюсов в левой полуплоскости неоднозначное, однако, как и в предыдущем случае, введение ограничений может сделать его однозначным. N ( p) не является функцией минимальной фазы. [31]
Теория, изложенная в этой главе, имеет общее значение и ее можно приложить к любому фильтру, обладающему характеристикой с равномерной пульсацией. Тип фильтра определяется лишь распределением полюсов. [32]
Нарушения непрерывности намагниченности в керамических образцах возникают из-за многочисленных пустот, включений и границ зерен. Это приводит к различным изменениям в распределении поверхностных полюсов, затрудняющих образование прямоугольной петли. Для получения прямоугольной петли магнитостатическая энергия этих зарядов Ml ( cos 6j - cos 62) 2 должна быть мала по сравнению с энергией, требуемой для создания доменов с обратной намагниченностью. [33]
Седловые точки на картине распределения нулей и полюсов замкнутой системы при любом значении коэффициента усиления и при единичной обратной связи находятся в тех же местах, где расположены седловые точки на картине распределения нулей и полюсов разомкнутой системы. При бесконечно большом коэффициенте усиления в картине распределения полюсов замкнутой системы останется только по диполю при каждом нуле, причем оси диполей, направленные от полюса к нулю, наклонены к оси а под углом, с которым траектория корней пересекает нуль. [34]
Чтобы корни характеристического уравнения реальной системы находились в этой области и система обладала степенью устойчивости не меньше заданной, а также колебательностью не больше установленной величины, необходимо надлежащим образом выбрать коэффициенты характеристического уравнения. В случае известных коэффициентов характеристического уравнения нужно уметь определять основные характеристики распределения полюсов передаточной функции без вычисления корней характеристического уравнения. [35]
Для решения этой задачи могут быть использованы корневые методы. Правила построения корневых годографов импульсных систем в плоскости z те же, что и в плоскости s для непрерывных систем, но связь распределения полюсов и нулей с показателями качества системы совершенно иная. Метод корневого годографа особенно эффективен для таких систем, характеристическое уравнение которых имеет пару комплексно-сопряженных корней с преобладающим влиянием на переходный процесс. [36]
Модель из эластичного листа, позволяющая представить амплитудную и фазовую характеристики. Хотя электрическая модель и дает количественно точный результат, все же она менее полезна, чем простая механическая модель, позволяющая видеть свойства распределения полюсов и нулей. Такая механическая модель представляет со: бой гибкий лист, растянутый на большом обруче. Вначале лист горизонтален, и если к нему приложить сосредоточенные вертикально направленные силы, то они отклонят лист от горизонтального направления, причем отклонения подчиняются при не слишком больших силах уравнению Лапласа. Высота листа относительно начального уровня будет соответствовать усилению а, линия пересечения листа с фиксированной вертикальной плоскостью, соответствующей оои / со, и наклон листа перпендикулярно оси / со будут соответствовать скорости изменения фазы вдоль оси / со. Точечные силы, представляющие собой полюсы и нули, должны быть равными по величине. Практически очевидная трудность, состоящая в том, что полюсы и нули суть математические точки и их, следовательно, надо представить такими силами, которые прокалывают лист, устраняется тем, что силы приложены через диски конечного диаметра, диаметр которых мал по сравнению с расстояниями между соседними полюсами и нулями. Подобный спо-со б вызывает с хорошей степенью приближения такие же деформации, как и приложение точечных сил. [37]
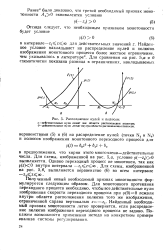 |
Расположение нулей и полюсов. [38] |
Полученный новый необходимый признак монотонности формулируется следующим образом. Для монотонного протекания переходного процесса необходимо, чтобы все действительные нули изображения скорости переходного процесса при р ( 0) 0 лежали внутри области расположения полюсов того же изображения, ограниченной справа вертикалью z - - - zr Найденный необходимый признак монотонности легко проверяется, если распределение полюсов изображения переходного процесса не задано. [39]
Пусть для переходного процесса & ( /) удовлетворяются все необходимые признаки монотонности. Выясним, какие из необходимых признаков монотонности удовлетворяются для всех функций Фп 1 ( /) ф 2 ( О - - - - - МО - Очевидно, что первый необходимый признак монотонности выполняется для всех функций, так как ближайший к мнимой оси полюс - гг из распределения полюсов не исключается. [40]
 |
Производная функции im ( / при it. 2 обращается в нуль, если предположить, что у (. 0 при / / j. [41] |
Итак, предположение о том, что для какого-либо значения l - tlt возможно т ( 00, привело к противоречию, а следовательно, Ф ( 0 0 во всем интервале 0 / оо. Таким образом, функция m ( f) монотонно убывает в интервале 0 / оо, если монотонно убывает функция Фш - i ( 0 - Так как в настоящее время прямыми вычислениями можно установить необходимые и достаточные признаки монотонного протекания функций bs ( f) только для s 3, то доказанная теорема применима к переходным процессам fyn ( f), если в распределении полюсов в левой полуплоскости соответствующих им изображений w ( z) не более двух комплексных сопряженных полюсов. [42]
Скажем нам не нравится, что конечный оператор может иметь нигде не используемые результаты. Мы второпях напишем: Распределение полюсов должно удовлетворять условию, чтобы конечный оператор не имел результатов. По принципу, сказав А, говорить и Б, мы должны будем, по-видимому, рассмотреть, описать и запретить другие случаи употребления операторов с неиспользуемыми операторами. [43]
В предыдущих параграфах показана замена ненаправленных звеньев направленными и приведено решение для общего случая схемы из направленных звеньев. Решение может быть получено либо классическим методом с помощью определителей, либо в упрощенном виде путем приведения любой блок-схемы к случаю одной главной цепи распространения энергии и множества цепей обратной связи. При этом каждый раз следует применять теорему 6 и находить распределение полюсов и нулей в s - плоскости. При исключении ответвлений прямой цепи и звеньев обратных связей сомножители эквивалентных блоков определяют с помощью изучения распределения нулей и полюсов. [44]
Сначала определяется функция распределения, которая дает требуемое поведение на оси / со, в предположении отсутствия внешних полюсов и нулей. Затем из приведенного выше уравнения находят отдельные функции распределения, необходимые для защиты окружности от каждого внешнего полюса или нуля. И, наконец, эти функции добавляют к первоначальному результату, после чего получается окончательная функция распределения полюсов. [45]
Страницы: 1 2 3 4