Распределение - прочность
Cтраница 1
Распределение прочности коротких участков волокон. [1]
Распределение прочности образцов при когезионном разрушении также следует нормальному закону Гаусса. [3]
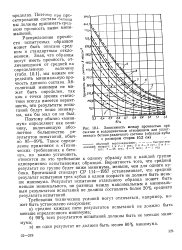 |
Зависимость между прочностью при сжатии и водоцементным отношением для уплотненного бетона различного состава ( образцы-кубы с размером сторон 10 2 см. [4] |
Распределение прочности испытуемых образцов может быть описано средним и стандартным отклонением. Зная, что образцы могут иметь прочность, отличающуюся от средней на определенную величину ( табл. 10.1), мы можем определить минимальную прочность данного состава. Абсолютный минимум не может быть определен, так как с точки зрения статистики всегда имеется вероятность, что результаты испытаний будут ниже минимума, как бы мал он ни был. [5]
Распределение прочности жестких пропиточных материалов может быть представлено нормальным законом. [6]
Пусть распределение прочности волокон в единичном объеме мерзлого торфа определяется кривой плотности вероятности. [7]
Законы распределения прочности на рис. 2.3 показывают, что по причине неоднородности структуры прочность в пределах агрегата может изменяться на порядок. Данное обстоятельство позволяет по - новому трактовать различие между расчетной и фактической ( реальной) прочностями неоднородных дисперсных систем. [8]
Природа распределения прочности изучалась рядом исследователей, и в [60] обнаружено три типа дефектов в стеклянных волокнах диаметром в 10 мкм. Там также приведено несколько графиков вероятностей разрушения и обсуждено их соответствие различным функциям распределения. III, в котором представлена модель временного разрушения, принято, что распределение прочности стеклянных волокон следует функции распределения Вейбул-ла [68], хотя некоторые исследователи и предпочитают распределение Гаусса. [9]
 |
Ориентационная прочности композиции. [10] |
Характеристиками распределения прочности группы волокон является средняя прочность и ее дисперсия. [11]
Зная закон распределения прочности материала, можно статистическими методами оценить прочность конструкции в тех случаях, когда ее разрушение наступает в результате разрушения ( происходящего с той или иной вероятностью) одного из нескольких элементов. На рис. 49 показаны функции распределения вероятностей разрушения пробок. [12]
Оценка параметров распределения прочности армирующих волокон, взаимодействующих по боковой поверхности, путем испытания их пучков / / Механика композитных материалов. [13]
После того как распределение прочностей отдельных элементов установлено, становится возможным в принципе вычисление распределения прочности комбинаций из таких элементов. [14]
 |
Расчетная схема пучка волокон, взаимодействующих по боковым поверхностям. [15] |
Страницы: 1 2 3 4 5
