Распределение - прочность
Cтраница 2
Для оценки функции распределения прочности волокон по результатам испытаний их пучков воспользуемся математической моделью, описывающей разрушение пучка при наличии взаимодействия между волокнами. Такие пучки являются частной моделью композита с матрицей низкой прочности. Однако для пучков слабо взаимодействующих волокон можно предложить более простую модель, позволяющую отразить физическую сущность явления и описать его аналитически. [16]
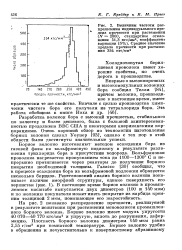
На рис. 2 показано распределение прочности, реализуемой в результате испытания при растяжении моноволокон промышленного борного волокна. Борное волокно имеет модуль упругости 40 070 - 40 770 кгс / мм2 и упругую, вплоть до разрушения, деформацию. Плотность борного волокна диаметром 140 мкм равна 2 55 г / см3 при комнатной температуре. [18]
На рис. 4.15 сопоставлено распределение прочности пучка моноволокон из Е - стекла с распределением прочности композиции из эпоксидной смолы, армированной прядью волокон из того же Е - стекла. [19]
Существенное влияние на кривую распределения прочности оказывает также действие на образец окружающей среды и способ его изготовления: механическая обработка граней образца или вытягивание его из расплава стекла, в результате которого в образце возникают термоупругие напряжения и анизотропия свойств по толщине. [20]
 |
Схемы к выводу формул статистической теории прочности наиболее слабого звена. [21] |
Выражение (3.14) определяет функцию распределения прочности цепи. [22]
На рис. 3 приведены ф-ции распределения прочности волоконных С. [23]
 |
Функция распределения прочности пробок. [24] |
На рис. 5.8 показаны функции распределения прочности пробок. [25]
Выражения вида (6.4), связывающие параметры распределения прочности и нагрузки со значением вероятности безотказной работы, называют уравнениями связи. Уравнение связи может быть использовано на этапе проектирования для расчета ожидаемого значения вероятности безотказной работы и решения других задач. Для этого выражение (6.4) приводят к виду, более удобному для применения на этом этапе. [26]
 |
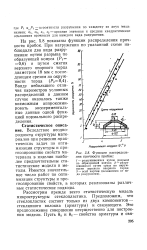
Распределение в координатах Вейбулла показателей прочности при растяжении образцов с длиной рабочей части 160 мм ( 1 и 40 мм ( 2. [27] |
Эксперименты показывают, что эмпирическая функция распределения прочности может быть аппроксимирована распределением Вейбулла, которое в координатах Вейбулла ( рис. 3.30) изображается в виде прямой линии. [28]
Ответ на поставленный вопрос дает сравнение распределения прочности моноволокон с распределением прочности композиции из таких же, параллельно уложенных волокон. На рис. 40 сопоставлено распределение прочности для пучка моноволокон из Е - стекла с распределением прочности композиции из эпоксидной смолы, армированной прядью волокон из того же Е - стекла. [29]
При этом одновременно должно произойти изменение распределения прочности связей. Задача определения этого распределения является фактически другим подходом к вопросам поляризации. [30]
Страницы: 1 2 3 4 5