Распределение - пуассон
Cтраница 2
Распределение Пуассона встречается в различных ситуациях. По Пуассону распределены, например, вызовы, поступающие на телефонную станцию, время ожидания в ресторанах или. [16]
Распределение Пуассона является предельным случаем биномиального распределения. Оно применимо в случаях, когда количество попыток ( л) приближается к бесконечности, а вероятность успеха ( р) - к нулю и математическое ожидание X пр - константа. [17]
Распределение Пуассона обладает важной отличительной особенностью: Х - единственный параметр, входящий в это распределение. Пуассона полностью определяется своим средним. [18]
Распределение Пуассона широко используется в теории массового обслуживания, контроле качества продукции и теории надежности. [19]
Распределение Пуассона сходится к нормальному распределению, когда его параметр стремится к бесконечности. [20]
Распределение Пуассона широко применяется при контроле производства и качества продукции. Точное решение возникающих при этом вопросов, как правило, дается формулами биномиального и нормального распределения; однако если доля брака р не больше 0 1, - а при надлежащей постановке производства доля брака значительно меньше этого числа, - то большая часть практических вопросов с достаточным приближением решается непосредственно при помощи распределения Пуассона. [21]
Распределение Пуассона получается также и в случае, когда точки распределяются случайным образом не на числовой оси, а на плоскости, поверхности или в пространстве. [22]
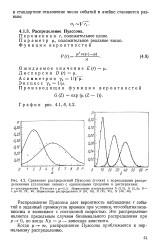 |
Сравнение распределений Пуассона ( точки с нормальными распределениями ( сплошные линии с одинаковыми средними и дисперсиями. [23] |
Распределение Пуассона дает вероятность наблюдения т событий в заданный промежуток времени при условии, что события независимы и возникают с пострянной скоростью. Это распределение является предельным случаем биномиального распределения при р - 0, но когда Np [ л - конечная константа. [24]
Распределение Пуассона является однопараметриче-ским и полностью определяется средней плотностью ( К), которая функционально связана со встречаемостью. [25]
Распределение Пуассона характерно для многих процессов, в которых значение признака образуется числом повторений некоторого явления в течение известного периода. Условие его образования состоит в возможности повторения этого явления через короткие промежутки времени, причем вероятность его не зависит от того, давно ли оно имело место в последний раз и сколько раз оно имело место. [26]
Распределение Пуассона и экспоненциальное распределение связаны друг с другом. [27]
Распределение Пуассона играет выдающуюся роль в теории вероятностей. Оно применяется при решении самых разных теоретических и прикладных задач. [28]
Распределение Пуассона применяется также при анализе надежности. [29]
Распределение Пуассона начинается, следовательно, всегда с нуля. [30]
Страницы: 1 2 3 4