Распределение - пуассон
Cтраница 3
Распределение Пуассона часто применяется тогда, когда значения признака ограничены с одной стороны и определяется число переходов через границу. [31]
Распределение Пуассона может быть получено преобразованием с помощью предельного перехода при п - оо дискретного биномиального распределения. [32]
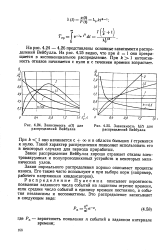 |
Зависимость a ( t для распределений Вейбулла.| Зависимость А ( 0 для распределений Вейбулла. [33] |
Распределение Пуассона описывает вероятность появления заданного числа событий на заданном отрезке времени, если среднее число событий в единицу времени постоянно, а события независимы и несовместимы. [34]
Распределение Пуассона применяется в том случае, когда имеют дело с числом появлений некоторого события при большом числе наблюдений и при малой вероятности наступления этого события в каждом отдельном наблюдении. [35]
Распределение Пуассона описывает поток событий, происходящих редко. Это соответствует условиям нормальной работы системы, когда интенсивность отказов постоянна. [36]
Распределение Пуассона является приемлемой моделью для описания случайного числа отказов и восстановлений объектов в фиксированном промежутке времени. [37]
Распределение Пуассона встречается при изучении размещения акцессорных минералов в изверженных горных породах. [38]
Распределение Пуассона касается случая редких событий. Им пользуются, когда число испытаний п велико, а вероятность р успеха мала, причем произведение пр имеет порядок нескольких единиц. [39]
Распределение Пуассона при больших п и п0 переходит в распределение Гаусса. [40]
Распределение Пуассона может быть получено из биномиального распределения путем предельного перехода при п - , / j - 0 при условии пр К const и в этом случае интерпретируется как закон редких явлений. Если п достаточно велико, а р мало, то формулу Пуассона ( 10) часто используют в качестве приближения вместо точных биномиальных формул для вероятностей k успехов в п испытаниях. [41]
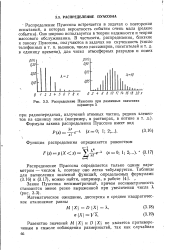 |
Распределение Пуассона при различных значениях параметра А. [42] |
Распределение Пуассона определяется только одним параметром - числом К, поэтому оно легко табулируется. [43]
Распределение Пуассона заслуживает особого внимания, так как из всех дискретных распределений оно наиболее часто встречается в приложениях. [44]
Распределение Пуассона называют еще распределением редких событий. Ему подчиняются случайные величины, вероятность появления которых в отдельном испытании мала и постоянна. [45]
Страницы: 1 2 3 4