Распределение - дискретная случайная величина
Cтраница 3
Функция р ( xi) называется законом распределения дискретной случайной величины. [31]
Функция р ( xj) называется законом распределения дискретной случайной величины. [32]
Функция распределения, в отличие от закона распределения дискретных случайных величин, является универсальной характеристикой случайной величины. [33]
Рассмотрим еще пример сопоставления эмпирического и теоретического распределений дискретной случайной величины. [34]
Функция р ( Xj) называется законом распределения дискретной случайной величины. [35]
Функция р ( Xf) называется законом распределения одномерной дискретной случайной величины. [36]
В предыдущем пункте мы показали, что функция распределения дискретной случайной величины изменяет свои значения только скачками. [37]
В настоящем параграфе приводятся наиболее часто встречающиеся типы распределений непрерывных и дискретных случайных величин и примеры их применения. [38]
Совокупность значений х и соответствующих вероятностей р называется распределением дискретной случайной величины. [39]
Требуется, используя критерий Пирсона, проверить гипотезу о распределении дискретной случайной величины X по биномиальному закону. [40]
Заданием возможных щ и соответствующих вероятностей Р - определяется закон распределения дискретной случайной величины X. Рассмотрим несколько примеров, для каждого из которых закон распределения случайной величины будет представлен в виде таблицы и графически. [41]
Совокупность значений Хь и соответствующих вероятностей р /, называется распределением дискретной случайной величины. [42]
 |
Законы распределения случайных величин. [43] |
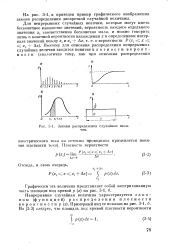
На рис. 3 - 1, а приведен пример графического изображения закона распределения дискретной случайной величины. [44]
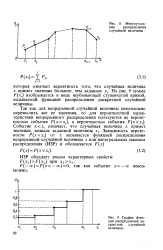 |
Многоугольник распределения случайной величины.| График функции распределения дискретной случайной величины. [45] |
Страницы: 1 2 3 4