Распределение - раис
Cтраница 1
Распределение Раиса обладает некоторой гибкостью и с помощью параметра р позволяет учесть возможные изменения закона распределения от нормального до закона Релея. Однако наличие одного регулировочного параметра в распределении Раиса не всегда обеспечивает необходимую гибкость в изменении вида функции распределения так, чтобы получить достаточно хорошую аппроксимацию наблюдаемого распределения. [1]
Распределение Раиса также имеет два параметра. Напомним, что s2 называется параметром нецентральности в эквивалентном хи-квадрат распределении. Он определяет мощность не замирающей сигнальной компоненты, иногда называемой зеркальной ( регулярной) компонентой принимаемого сигнала. [2]
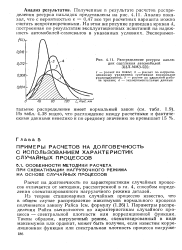 |
Распределение ресурса накладок сцепления автомобилей ЗИЛ-ММЗ-555. [3] |
Параметры распределения Раиса вычисляются по характеристикам случайного процесса - спектральной плотности или корреляционной функции. [4]
И распределение Релея, и распределение Раиса часто используется да описания статистики флуктуации сигнала на выходе многопутевого канала с замираниями. Эта модель канал рассматривается в гл. Другое распределение, часто используемое для характеристики статистию сигналов, передаваемых через многопутевые каналы с замираниями - это от-распределение Накагами. [5]
Дальнейшая обработка с целью получения параметров распределения Раиса может осуществляться двумя путями. [6]
Более корректным является расчет с использованием распределения Раиса. [7]
Распределение (2.86) называют обобщенным релеевским или распределением Раиса. На рис. 2.7 показаны графики этого распределения. [8]
 |
Распределение фазы. [9] |
Распределение (2.86) называют обобщенным релеевским распределением или распределением Раиса. [10]
Нов о л о цк а я С. А. Таблицы функции распределения Раиса. [11]
В то время как распределение Релея связано с центральным хи-квадрат-распределением, распределение Раиса связано с нецентральным хи-квадрат-распределением. [12]
Плотность вероятности огибающей ( 22) соответствует обобщенному закону Релея или распределению Раиса. [13]
Распределение Накагами позволяет описать более широкий класс распределений, чем, например, распределение Раиса. [14]
Бесселя нулевого порядка, erf - функция ошибок, a p ( Z) известно как распределение Раиса. Отметим, что ( ф 0, как и ожидалось, поскольку значение фазы V было положено равным нулю. [15]
Страницы: 1 2