Распределение - расстояние
Cтраница 2
В настоящей статье выведены, исходя из распределения расстояний, некоторые свойства кодов. Материал расположен следующим образом. Кравчука напоминаются определение и некоторые свойства формального преобразования Мак-Вильяме. Затем на основании распределения расстояний кода и его преобразования Мак-Вильяме вводятся четыре параметра. [16]
Вводя дальнейшие предположения о том, что распределение расстояний между узлами этой сетки описывается гаус совой функцией распределения и что при деформации все расстояния между узлами изменяются подобно общей деформации тела, кинетическая теория позволяет вычислить изменение числа конгЬормаций сетки при изотермическом переходе от недеформированного состояния к деформированному. [17]
А ( С ] - преобразование Мак-Вильяме распределения расстояний и обозначает эрмитову норму. [18]
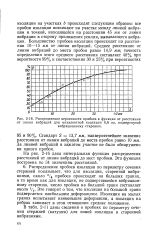 |
Распределение вероятности пробоев в функции от расстояния. [19] |
На рис. 2 - 16 дана интегральная функция распределения расстояний от линии вибраций до мест пробоев. Эта функция построена по 34 значениям расстояний. [20]
Ширина этих полос незначительно увеличивается при повышении температуры, потому что распределение расстояний между ближайшими соседними молекулами становится более размытым при более высоких температурах. [21]
Последним направлением усовершенствования упрощенной теории гауссовых цепей является использование пространства для описания распределения расстояний между концами цепи в так называемой обратной функции Ланжевена. Гауссова функция распределения применима только тогда, когда расстояние между концами цепи много меньше контурной длины молекулы. [22]
Следовательно, теорема доказывается индукцией по т, так как р полностью определяется распределением расстояний кода С. [23]
По определению это число равно i - й компоненте Лг - ( С) распределения расстояний. Начиная с этого места, будем предполагать, что все коды содержат нулевую - последовательность над F это не будет существенным ограничением, так как любой код можно преобразовать в код, обладающий этим свойством, применяя подходящий сдвиг группы G Fn, который не меняет расстояния между кодовыми словами. Таким образом, для кодов, метрически инвариантных, распределение расстояний сводится к классическому распределению весов. [24]
Используя уравнение (5.50), можно рассчитать дихроизм отдельной цепи, а с помощью функции распределения расстояний между концами цепи относительно направления растяжения можно определить дихроизм полос ориентированного полимера. Эта функция распределения была рассчитана [943] при предположении об афинной деформации макромолекулярной сетки при ее растяжении. [25]
Распределение расстояний между узлами сетки по формуле ( 22) совпадает по форме с распределением расстояний между концами цепей согласно Куну-Марку - Гуту по уравнению ( 15) и соответствует распределению величин отрезков по закону случая. Кроме того, Уолл вводит предположение о том, что компоненты длины каждого отрезка при деформации изменяются так же, как и размеры тела. [26]
Усредненное по большим промежуткам времени ( скажем, 10 - 8 с или более) распределение расстояний до соседних молекул от любой данной молекулы в жидкости не является случайным. [27]
Имея в основе макромолекулу углевод орода с п связями, требуется найти, например, распределение расстояний между первым и последним атомом углерода, зная, что большое количество комбинаций может находиться в зависимости от ограниченного вращения около С - С связей. После того как будет установлено некоторое количество связей в углеводородной цепи, направление последующих связей уже не зависит от тех направлений, по которым были установлены первые связи. Можно отметить, что углеводородная цепь состоит из N свободно вращающихся сегментов, состоящих в свою очередь из s связей. Положение каждого сегмента в пространстве не зависит от положения предыдущего сегмента и каждое положение одинаково вероятно. [28]
В действительности всегда происходит наложение релаксационных процессов обоих типов, и граница между ними размыта существованием распределения расстояний между узлами сетки и различием их природы в реальном материале. Это, в частности, приводит к тому, что при течении, происходящем с определенной скоростью, часть узлов сохраняется в виде квазистабильной сетки, а часть оказывается распавшимися достаточно быстро, чтобы их присутствие было несущественным для сопротивления течению материала. Поэтому в зависимости от скорости внешнего воздействия реакция системы на это воздействие может оказаться совершенно различной. [29]
Сравнение приведенных кривых и сопоставление соответствующих им фотографий шлифов показывают, что структура норового пространства отражается на форме кривой плотности распределения расстояний между зернами породы. Очевидно, меньшему значению дисперсии D кривых соответствует более однородное строение пор. [30]
Страницы: 1 2 3 4