Распределение - вероятность
Cтраница 4
Распределение вероятностей с такой плотностью принято называть - распределением ( хи-распределением) с п степенями свободы. [46]
Распределение вероятностей (10.35) позволяет вычислить различные статистические характеристики, связанные с коэффициентом отражения. [47]
Распределения вероятностей (10.187) позволяют вычислить статистические характеристики коэффициентов отражения для падающих волн. [48]
Распределение вероятностей, определяемое формулой (1.36), называется полиномиальным. [49]
Распределение вероятностей, определяемое этой формулой, называется вырожденным нормальным распределением. [50]
Распределение вероятностей, определяемое этой формулой, называется распределением арксинуса. [51]
Распределение вероятностей, которое дается формулой (7.5), называют биномиальным распределением, или распределением Бернулли. [52]
Распределение вероятностей для координат в стационарном состоянии определяется квадратом п 2 tyn 2; мы видим, что оно не зависит от времени. [53]
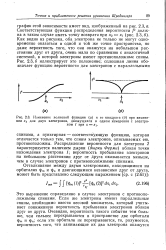 |
Изменение волновой функции ( а и ее квадрата ( б при изменении х2 для двух электронов, движущихся в одном измерении с электроном / при х х. [54] |
Распределение вероятности для электрона 2 характеризуется наличием дырки ( дырки Ферми) вблизи точки нахождения электрона /; вероятность пребывания электронов на небольшом расстоянии друг от Друга оказывается меньше, чем в случае электронов с противоположными спинами. [55]
Страницы: 1 2 3 4