Распределение - вероятность - случайная величина
Cтраница 3
В табл. П 1.1 приведены функции распределения вероятностей случайных величин, используемые в теории надежности, и основные данные для них. [31]
Рассмотрим вопрос о том, как меняется распределение вероятностей случайных величин при том или ином преобразовании. [32]
Во многих экспериментах мы заранее не знаем распределения вероятностей случайной величины. Например, в задаче о статистике зрелищных мероприятий до проведения опроса неизвестны доли людей, регулярно посещающих кинотеатры и смотрящих телевизионные программы. Поэтому мы не можем использовать имеющуюся заранее информацию для предсказания результатов опроса, а вынуждены поступать наоборот: мы используем результаты опроса для оценки долей людей, входящих в каждую из четырех возможных групп. Другой пример: пусть нам требуется оценить распределение вероятностей для случайной величины - роста американского гражданина в возрасте 20 лет. Полный анализ роста всех американских граждан в возрасте 20 лет обойдется очень дорого и займет много времени. Поэтому мы основываем анализ на рассмотрении некоторой выборки; выводы относительно среднего роста и разброса величины роста для всей совокупности 20-летних американских граждан основываются на соответствующих данных, полученных для этой выборки. [33]
Нормальное распределение ( normal distribution) - распределение вероятностей случайной величины, являющееся унимодальным и описываемое колоколообразной ( симметричной) кривой; его средняя ( математическое ожидание) совпадает с модой. [34]
Для решения практических инженерных задач помимо функции распределения вероятностей случайной величины необходимо узнать отдельные параметры распределения. Эти параметры определяются по соответствующим правилам из функции распределения. Среди этих параметров наиболее важными, играющими основную роль в применении к решению задач по определению показателей ремонтопригодности и технического обслуживания трубопроводов, являются две числовые характеристики случайных величин: математическое ожидание и дисперсия. [35]
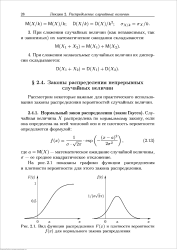 |
Вид функции распределения F ( x и плотности вероятности f ( x ] для нормального закона распределения. [36] |
Рассмотрим некоторые важные для практического использования законы распределения вероятностей случайных величин. [37]
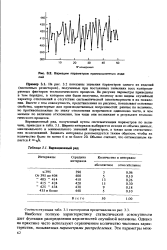 |
Вариации параметров промышленных изделий.| Вариационный ряд. [38] |
Наиболее полную характеристику статистической совокупности дает функция распределения вероятностей случайной величины. Однако на практике часто используют ограниченное количество числовых характеристик, называемых параметрами распределения. [39]
Функция ср ( лт) называется плотностью распределения вероятностей случайной величины X, произведение y ( x) dx - элементом вероятности. Кривая у ср ( дг) называется кривой распределения вероятностей данной случайной величины. [40]
Функция ф ( х) называется плотностью распределения вероятностей случайной величины X, произведение ф ( х) dx - элементом вероятности. Кривая у ф ( х) называется кривой распределения вероятностей данной случайной величины. [41]
Функция F ( x) названа функцией распределения вероятности случайной величины X. [42]
Функция ф ( х) называется плотностью распределения вероятностей случайной величины X, произведение ф ( х) dx - элементом вероятности. Кривая у ф ( х) называется кривой распределения вероятностей данной случайной величины. [43]
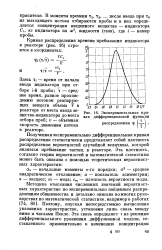 |
Экспериментальная кривая дифференциальной функции. [44] |
Полученная экспериментально дифференциальная кривая распределения статистически представляет собой плотность распределения вероятностей случайной величины, которой является пребывание частиц в реакторе. [45]
Страницы: 1 2 3 4