Распределение - система
Cтраница 1
Распределение систем по состояниям задается совокупностью чисел Mi, указывающих число систем в состоянии i. Каждое распределение может быть осуществлено определенным числом способов. Очевидно, что, как и в статистике молекул Больцмана и в этом случае должно иметь место наиболее вероятное распределение, осуществляемое наибольшим числом способов. Чтобы найти это распределение, необходимо определить максимум числа способов ( w) осуществления распределения. [1]
Распределение системы представляют собой с формальной точки зрения совокупность взаимодействующих процессов. Присущий природе взаимодействия параллелизм и сложные причинно-следственные связи порождают ряд проблем, которые могут повлиять на эффективность функционирования распределенной системы и даже на правильность функционирования. Для проверки правильности функционирования распределенных систем используют моделирование. Построение модели распределенной системы и ее анализ позволят исследовать свойства системы и могут дать информацию о причинах неудовлетворительного функционирования. [2]
Распределение системы независимых случайных величин вполне определяется их индивидуальными распределениями. [3]
Рассмотрим распределение систем по квантовым состояниям. [4]
Возможно распределение системы на несколько компьютеров, как ядра, так и сервисов или построение кластера для обеспечения ее бесперебойной работы. [5]
Если распределение системы любого числа п сечений случайной функции X ( t) нормальное, то случайная функция называется нормальной; характеристики Kx ( t, t) и mx ( t) являются для нее исчерпывающими. [6]
Функция распределения системы нескольких случайных величин вводится как обобщение функции распределения системы двух случайных величин. [7]
Функция распределения системы ( х, у) представляет собой функцию от двух аргументов. [8]
Закон распределения системы двух случайных величин X, У определяется распределением каждой из величин, входящих в систему, и зависимостью между ними. Степень зависимости случайных величин X и К характеризуется условным законом распределения, под которым понимается закон распределения одной из случайных величин, найденный при условии, что другая случайная величина приняла определенное значение. [9]
Возможность распределения системы е пространстве существенно уменьшает затраты на кабельные линии. Использование наборов программ и специализированных языков позволяют привязать систему управления к конкретному объекту при минимальных затратах временя. Для этого этапа характерны отсутствие локальных средств резервирования ц - наличие развитых средств представления информации технологу-оператору. Даже при небольшой размерности стоимость системы цифрового управления сравнима со стоимостью систем, построенных на средствах локальной автоматизации: однако СЦУ обладают боль-шими возможностями. [10]
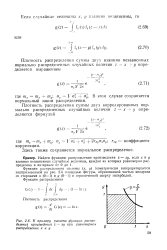 |
К примеру расчета функции распре деления произведения z ху при равномерном распределении х и у. [11] |
Функция распределения системы ( х, у) геометрически интерпретируется заштрихованной на рис. 2.6 площадью фигуры, образованной частью квадрата со сторонами х ( 0 - 1) и у ( 0 - 1) и ограниченной сверху гиперболой. [12]
Функция распределения системы (11.1) равна, очевидно, произведению функций (11.2) всех осцилляторов. [13]
Результаты распределения систем приведены в таблице. [14]
Закон распределения системы двух случайных величин является функцией двух аргументов. [15]
Страницы: 1 2 3 4