Распределение - продольная скорость
Cтраница 2
Интегральные толщины ( 28) и возможные другие представляют функционалы распределений продольных скоростей в сечениях пограничного слоя. Численные величины этих функционалов могут быть определены только после полного решения конкретной задачи, между тем как в излагаемом далее методе подобия толщина пограничного слоя входит в самом начале при составлении безразмерной формы искомого решения. [16]
Чтобы подсчитать полный расход через сечение рассматриваемой плоской струи, примем, что формула распределения продольных скоростей по сечению струи (8.22) остается справедливой и для того случая, когда ширина струи асимптотически стремится к бесконеч. [17]
Переход ламинарного пограничного слоя на пластине в турбулентный сопровождается изменением законов нарастания толщины пограничного слоя и распределения продольных скоростей. Можно видеть, что при Res3 2 - 105 безразмерная толщина слоя постоянна и приблизительно равна пяти. При больших Re, она заметно возрастает по почти линейному закону. [18]
Если при решении дифференциальных уравнений пограничного слоя ( VII-10) искомой является функция wx f ( y) распределения продольной скорости wx по толщине пограничного слоя, то при решении интегральных соотношений ( VII-13, VII-15) эта функция выбирается произвольно. [19]
Учет инерциальных сил довольно сложен в общем случае пространственного нестационарного обтекания тела, так как при подсчете массы газа в данном сечении возмущенного слоя и распределения продольных скоростей в нем необходимо следить за траекториями частиц, зависящими, по крайней мере, от двух переменных: координат и времени. [20]
Со времени сообщения А. Я. Миловича о его опытах по движению поплавков на поверхности открытого потока жидкости в изогнутом лотке прямоугольного сечения ( 1912) внимание многих исследователей привлекал вопрос: подчиняется ли распределение продольных скоростей на повороте закону площадей. [21]
Таким образом, одна из основных предпосылок, принятых по постановке задачи ( отсутствие обратного влияния пограничного слоя на внешнее течение: t / const Uoo) означает только, что в принятом приближении возникновение пограничного слоя не искажает распределения продольной скорости во внешнем потоке, хотя и вызывает в нем слабое поперечное течение. [22]
 |
Профили скорости и температуры ( влияние вдувания и отсасывания через проницаемые границы. [23] |
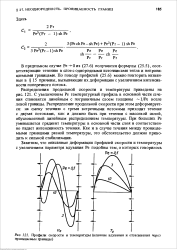
С увеличением Ре температурный профиль в основной части сечения становится линейным с пограничным слоем толщины - 1 / Ре возле левой границы. Распределение продольной скорости при этом деформируется: на смену течению с тремя встречными потоками приходит течение с двумя потоками, как и должно быть при течении с массовой силой, обусловленной линейным распределением температуры. При больших Ре уменьшается градиент температуры в основной части слоя и соответственно падает интенсивность течения. Как и в случае течения между проницаемыми границами разной температуры, это обстоятельство должно приводить к сильной стабилизации. [24]
 |
Линии равных скоростей и схема вторичных течений для полностью развитого потока в трубах некруглого сечения. [25] |
Большинство других типов поперечных сечений, если даже их форма и размер не меняется по длине трубы или канала, формируют турбулентные течения, которые отличаются от двумерных течений в случае круглых или широких прямоугольных поперечных сечений. Распределение продольных скоростей носит трехмерный характер, особенно вблизи углов. [26]
При движении жидкости вдоль плоской поверхности профиль распределения продольной скорости поперек потока изменяется по мере удаления от передней кромки пластины. Если скорость в ядре потока и 0, то основное изменение ее происходит в пограничном слое толщиной S, где скорость уменьшается от vv0 до wx 0 на поверхности пластины. Течение в пограничном слое может быть как ламинарным, так и турбулентным. Режим течения определяется критическим значением критерия Рейнольдса, нижний предел которого для ламинарного пограничного слоя равен ReKp 8 10, а при Re 3 106 вдоль пластины устанавливается устойчивый турбулентный режим течения. [27]
Оно позволяет установить поперечный компонент осредненной скорости, если известно распределение продольных скоростей. [28]
 |
Ламинарный пограничный слой длиной х - хко. [29] |
Если при решении дифференциальных уравнений пограничного слоя (24.2) искомой является функция wx - f ( y) распределения продольной скорости wx по толщине пограничного слоя, то при решении интегральных соотношений (24.4), (24.5) эта функция выбирается произвольно, но так, чтобы граничные условия на поверхности тела и на внешней кромке пограничного слоя были удовлетворены. [30]
Страницы: 1 2 3