Распределение - продольная скорость
Cтраница 3
Однако это решение не удовлетворяет основному требованию, предъявляемому к определению толщины пограничного слоя, которое было установлено в самом начале предыдущего параграфа. Это требование, напомним, заключается в том, что понятие толщины пограничного слоя неразрывно связано с распределением продольных скоростей в сечениях внутри пограничного слоя и должно количественно представляться функционалом этого распределения. [31]
Если при решении дифференциальных уравнений пограничного слоя (7.10) искомой является функция wx - - f ( y) распределения продольной скорости wx по толщине пограничного слоя, то при решении интегральных соотношений (7.12), (7.13) эта функция выбирается произвольно, но так, чтобы граничные условия на поверхности тела и на внешней кромке пограничного слоя были удовлетворены. [32]
Такая характерная для метода подобия обратная связь между количественным определением толщины пограничного слоя и решением конкретной задачи, требующая пересчета этой толщины от одного приближения к другому, служит повышению быстроты сходимости приближений. Пренебрежение этим обстоятельством в известных методах Блазиуса, Гертлера и др., не использующих связь между масштабом ординат и распределениями продольных скоростей в сечениях пограничного слоя, служит, по-видимому, главной причиной медленной сходимости приближений в этих методах. [33]
На основании своих экспериментов в лотках с различной формой поперечного сечения он заключил, что закон площадей в точности не выдерживается даже для лотка прямоугольного поперечного сечения и полностью нарушается в лотках трапецеидального и треугольного сечений. Распределение продольных скоростей по ширине потока, как показали эксперименты Кожевникова, в большой мере зависит от формы поперечного сечения потока, и, следовательно, ошибочно искать общую закономерность для распределения продольных скоростей без учета формы поперечного сечения. К такому же выводу пришел позднее И. Л. Розовский, который, как уже отмечено, выполнил и теоретический анализ этого вопроса. [34]
В этих работах получены траектории частиц при поперечном обтекании запыленным потоком пластины конечной толщины. Распределения продольной скорости газа в присутствии частиц различных размеров и самих частиц без учета их отражения от поверхности тела, полученные в [12], показаны на рис. 5.10. Из приведенных данных видно, что скорости газовой и дисперсной фаз сильно различаются. С увеличением инерционности частиц их скорость на поверхности пластины возрастает. Присутствие в потоке крупных частиц оказывает большее влияние на распределение скорости несущего газа в области торможения. [35]
Под толщиной пограничного слоя как некоторой конечной величины 6 подразумевают расстояние от поверхности обтекаемого тела до такой точки в потоке ( у 6), где практически, с любой наперед заданной степенью приближения можно принять продольную скорость в пограничном слое равной ее значению в той же точке безвихревого потока, или завихренность равной нулю. Геометрическое место таких точек дает приближенное, конечное представление о внешней границе пограничного слоя. Отмеченная асимптотичность распределений продольных скоростей и завихренности в области пограничного слоя сближает понятия пограничного слоя конечной толщины с асимптотическим слоем. [36]
Эта теория была разработана для турбулентных свободных струй. Суть ее сводится к следующему. Отметив, что распределение полной продольной скорости в поперечных сечениях зоны смешения струи следует кривой Гаусса, Рейхард предположил, что процесс турбулентного переноса является статистическим и в точности аналогичен процессу молекулярного переноса. Следовательно, дифференциальное уравнение, описывающее изменение oi2, должно быть идентично уравнению молекулярной диффузии. Значит, надо преобразовать уравнение движения так, чтобы получить уравнение диффузии. [37]
Эта теория была разработана для турбулентных свободных струй. Суть ее сводится к следующему. Отметив, что распределение полной продольной скорости в поперечных сечениях зоны смешения струи следует кривой Гаусса, Рейхард предположил, что процесс турбулентного переноса является статистическим и в точности аналогичен процессу молекулярного переноса. Следовательно, дифференциальное уравнение, описывающее изменение coj2 должно быть идентично уравнению молекулярной диффузии. Значит, надо преобразовать уравнение движения так, чтобы получить уравнение диффузии. [38]
Розовский ( 1957, 1960) более обстоятельно, чем другие авторы, изучил вопросы, связанные с трехмерностью течения на закруглении руслового потока, однако и его анализ является весьма приближенным и направлен, как правило, на изучение каждой из особенностей кинематики такого потока по отдельности. Им рассмотрены, в частности развитие поперечной циркуляции на изгибе потока и распределение продольных скоростей в зоне изгиба. [39]
На основании своих экспериментов в лотках с различной формой поперечного сечения он заключил, что закон площадей в точности не выдерживается даже для лотка прямоугольного поперечного сечения и полностью нарушается в лотках трапецеидального и треугольного сечений. Распределение продольных скоростей по ширине потока, как показали эксперименты Кожевникова, в большой мере зависит от формы поперечного сечения потока, и, следовательно, ошибочно искать общую закономерность для распределения продольных скоростей без учета формы поперечного сечения. К такому же выводу пришел позднее И. Л. Розовский, который, как уже отмечено, выполнил и теоретический анализ этого вопроса. [40]
Поэтому для снижения влияния инерционных сил и сокращения длины выравнивания потока на закрытом участке в пучках теплообменников предусматривают специальные меры. Так, в ПТО реактора БОР-60 поток ниже входных окон дросселируется в специальных дистанционирующих решетках. Ребра предназначены для гашения продольной составляющей скорости в центре пучка, так как при небольшой глубине пучка ( и числе рядов около 10) и большой поперечной скорости на входе неравномерность в распределении продольной скорости может быть весьма значительной. В теплообменнике установки CRFBR поток теплоносителя при входе в трубный пучок ( на выходе из кольцевого зазора) дросселируется в наклонной перфорированной решетке. [41]
Выражение (3.35) имеет весьма общий характер. Подставляя в него различные профили скорости и коэффициенты переноса ( диффузии), можно получить эффективные коэффициенты для различных видов течения жидкости в трубе. Из выражения (3.35) отчетливо видно, что эффективный коэффициент диффузии нельзя отождествлять с коэффициентами молекулярной и турбулентной диффузии, этот параметр интегрально учитывает как диффузионные, так и конвективные процессы переноса. Отсюда же следует, что эффективный коэффициент диффузии зависит от распределений продольной скорости и и коэфициента переноса е по сечению трубы. [42]
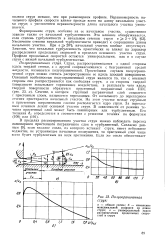 |
Полуограниченная струя. [43] |
Формирование струи, особенно на ее начальном участке, существенно зависит также от начальной турбулентности. Увеличение степени начальной турбулентности приводит к сокращению длины начального участка. При е 20 % начальный участок вообще отсутствует. Заметим, что начальная турбулентность практически не влияет на характер распределения продольных скоростей в пределах основного участка струи. Профили продольных скоростей остаются универсальными, как и в случае струи с низкой начальной турбулентностью. [44]
Для задачи обтекания кругового цилиндра такого рода расчеты были выполнены рядом зарубежных ученых в 1953 - 1959 гг. Результаты численных решений совпали с известной экспериментальной картиной образования в следе за цилиндром и сферой пары замкнутых зон обратных ( вторичных) течений, обычно неточно именуемых вихрями. Была показано, что продольные размеры этих зон растут с рейнольдсовым числом, в то время как поперечные почти от него не зависят. Наряду с чисто динамическими были рассмотрены и тепловые задачи. Особый интерес представляет та часть этой общей проблемы, которая относится к потере устойчивости симметричного обтекания тела и переходу к нестационарной картине поочередного отделения зон замкнутых обратных течений от поверхности тела и сворачивания их в вихри. Этот доклад, так же как и предыдущая работа Фромма, был посвящен исследованиям в области динамики вязкой жидкости при малых и средних рейнольдсовых числах. Было изучено нестационарное обтекание плоской пластинки, расположенной перпендикулярно к потоку. Составленный по этим отдельным кадрам фильм был продемонстрирован на симпозиуме и показал отчетливув картину развития явлений в следе за пластинкой. Отметим, что определенные расчетным путем сопротивление пластинки, влияние на сопротивление ширины потока, распределения продольных скоростей в следе за пластинкой оказались при этом хорошо совпадающими с соответствующими экспериментальными результатами. Замечательно, что машинные расчеты позволили вполне удовлетворительно определить число Стру-хала образования сходящих с пластинки вихрей и даже зависимость - этого числа от числа Рейнольдса. Таким образом, точное решение уравнений Навье - Стокса на электронно-вычислительных машинах становится практическим методом исследования движений вязких жидкостей при малых и средних значениях рейнольдсовых чисел. [45]
Страницы: 1 2 3