Распределение - индуктивная скорость
Cтраница 1
Распределение индуктивных скоростей равномерное. [2]
 |
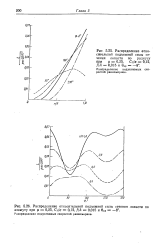
Сопоставление экспериментальных величин поперечного наклона конуса лопастей с величинами, рассчитанными при Ст / a 0 08, апкл 1 и различных распределениях индуктивных скоростей ГН. 48 ]. [3] |
На рис. 5.39 видно, что учет неравномерности распределения индуктивных скоростей действительно приводит к более правильной оценке PIS как по величине, так и по характеру изменения в зависимости от ц, но все-таки поперечный наклон ПКЛ получается существенно заниженным. Это на - водит на мысль, что теория несущего винта не позволяет пока надежно рассчитать даже первые гармоники неравномерного распределения индуктивной скорости, которые определяют наклон ПКЛ. [4]
Высшие гармоники махового движения лопасти возникают в основном вследствие неравномерности распределения индуктивных скоростей. Здесь был рассмотрен только частный случай - линейное распределение. В общем случае высшие гармоники махового движения имеют значительно большие амплитуды, чем получено выше. Кроме того, для лучшего согласования расчетов высших гармоник с экспериментом нужно учесть изгибные Колебания лопасти. Высшие гармоники махового движения обычно слабо сказываются на аэродинамических характеристиках несущего винта и характеристиках управления, но они играют главную роль в вибрациях вертолета и нагрузках лопасти. [5]
Сделаны следующие предположения: каждое сечение лопасти обтекается двумерным стационарным потоком, распределение индуктивных скоростей равномерное, влиянием радиального течения можно пренебречь, лопасть совершает только маховое движение как твердое тело вокруг оси отнесенного ГШ. Предположения о малости углов не делалось. [6]
Таким образом, расхождение теоретических и экспериментальных результатов обусловлено главным образом неравномерностью распределения индуктивных скоростей при полете вперед. [7]
 |
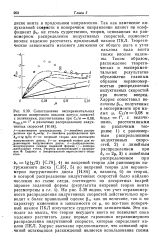
Графики характеристик несущего винта по Тэниеру [ Т. 14, Т. 15 ]. [8] |
В этой теории приняты следующие допущения: аэродинамические коэффициенты сечений лопасти совпадают с экспериментальными коэффициентами профиля в стационарном потоке, распределение индуктивных скоростей равномерное, радиальным течением можно пренебречь, лопасть абсолютно жесткая и совершает только маховое движение. [9]
Эта формула определяет требуемую мощность как функцию полетной массы или скорости. Расчет характеристик можно уточнить, если учесть неравномерность распределения индуктивных скоростей, ввести в расчет действительные значения коэффициентов сопротивления сечений ( для чего нужно знать распределение углов атаки по диску винта) и более детально определить сопротивление вертолета. В расчетах CQ, часто учитывалось распределение углов атаки сечений по диску. [10]
Авторы рассматривали шарнирный винт, лопасти которого имеют неоперенную часть, произвольную крутку и произ вольное распределение хорд. Распределение индуктивных скоростей было принято линейным, а угол взмаха р - малым. [11]
Присоединенным вихрям, циркуляции которых определяют подъемную силу крыла конечного размаха, соответствуют свободные вихри, сходящие с крыла и образующие его след, Нагрузка лопасти наиболее сильно изменяется в ее концевой части. Поэтому завихренность в следе несущего винта концентрируется в спиралеобразные концевые вихри, расположенные под винтом. В отличие от крыла лопасть проходит очень близко от собственного следа и от следов предшествующих лопастей. Близость следа оказывает значительное влияние на распределения индуктивных скоростей и нагрузки лопасти. Вихревая теория представляет собой исследование работы несущего винта, в котором на основе законов гидродинамики, определяющих движение и воздействие завихренности ( формула Био - Савара, теоремы Кельвина и Гельмгольца), рассчитывается индуцируемое следом винта поле скоростей и, в частности, распределение индуктивных скоростей по диску винта. В простейшем варианте вихревой теории использована схема активного диска. Это означает, что не учитывается дискретность самого винта и его следа, связанная с конечным числом лопастей, а завихренность непрерывно распределяется по пространству, занятому следом. Если рассматривать ту же схему течения, что и в импульсной теории, то вихревая теория должна, конечно, дать такие же результаты. Однако вихревая теория лучше, чем импульсная, пригодна для обобщений схемы течения ( например, учета неравномерности нагрузки на диск), так как она связана с рассмотрением местных, а не обобщенных характеристик. [12]
Так как индуктивная скорость w распределена равномерно, скачок Ар давления также постоянен на диске винта. Однако из условия р2 0 / 2) p ( V u) 2 const не следует, что давление и особенно индуктивная скорость на диске винта должны быть распределены равномерно. Таким образом, хотя сделанные в разд. Ар и w оправданы, импульсная теория не дает никаких указаний о распределении индуктивной скорости по диску винта. Этот результат аналогичен тому, который получают в плоскости Треффца при исследовании обтекания крыла. Такое исследование показывает, что индуктивное сопротивление минимально при равномерном скосе потока в дальнем следе и эллиптической нагрузке крыла, но ничего не говорит в распределении индуктивных скосов по крылу. [13]
Общая теория воздушного винта была разработана в начале 1920 - х годов на базе вихревой теории и прандтлевской теории крыла. Путем введения в расчет индуктивных скоростей, определяемых вихревой теорией, были найдены аэродинамические параметры потока на диске несущего винта. Поэтому в теорию элемента лопасти теперь обычно вводят индуктивные скорости, получаемые по импульсной теории. Последняя не смогла объяснить распределение индуктивных скоростей по диску несущего винта, которое требовалось для завершения разработки теории элемента лопасти. В результате вихревую теорию стали считать более надежной и логичной основой для исследования работы как крыльев, так и лопастей. [14]
Присоединенным вихрям, циркуляции которых определяют подъемную силу крыла конечного размаха, соответствуют свободные вихри, сходящие с крыла и образующие его след, Нагрузка лопасти наиболее сильно изменяется в ее концевой части. Поэтому завихренность в следе несущего винта концентрируется в спиралеобразные концевые вихри, расположенные под винтом. В отличие от крыла лопасть проходит очень близко от собственного следа и от следов предшествующих лопастей. Близость следа оказывает значительное влияние на распределения индуктивных скоростей и нагрузки лопасти. Вихревая теория представляет собой исследование работы несущего винта, в котором на основе законов гидродинамики, определяющих движение и воздействие завихренности ( формула Био - Савара, теоремы Кельвина и Гельмгольца), рассчитывается индуцируемое следом винта поле скоростей и, в частности, распределение индуктивных скоростей по диску винта. В простейшем варианте вихревой теории использована схема активного диска. Это означает, что не учитывается дискретность самого винта и его следа, связанная с конечным числом лопастей, а завихренность непрерывно распределяется по пространству, занятому следом. Если рассматривать ту же схему течения, что и в импульсной теории, то вихревая теория должна, конечно, дать такие же результаты. Однако вихревая теория лучше, чем импульсная, пригодна для обобщений схемы течения ( например, учета неравномерности нагрузки на диск), так как она связана с рассмотрением местных, а не обобщенных характеристик. [15]
Страницы: 1 2