Распределение - циркуляция
Cтраница 3
Однако большие трудности возникают при определении дополнительной индуцированной скорости ws, которая зависит от распределения циркуляции вдоль размаха. [31]
Теория Прандтля основана на рассмотрении системы П - образных вихрей и приводит к интегро-дифференциальному уравнению для распределения циркуляции вихря вдоль несущей линии крыла. Исследования приближенных методов решения интегро-дифференциального уравнения крыла конечного размаха были начаты в Германии еще А. [32]
Итак, при принятых условиях геометрической незакрученности и одинаковости аэродинамических характеристик вдоль размаха, крыло с эллиптическим распределением циркуляции будет иметь и эллиптическую форму в плане, подобную кривой распределения циркуляции; такое крыло может быть названо эллиптическим. [33]
Итак, при принятых условиях геометрической незакрученности и одинаковости аэродинамических характеристик вдоль размаха, крыло с эллиптическим распределением циркуляции будет иметь и эллиптическую форму в плане; такое крыло может быть названо эллиптическим. [34]
Как и в случае безграничной жидкости, задача, следовательно, состоит в том, чтобы установить распределение циркуляции. [35]
Аналогично вычисляют все остальные коэффициенты апт, а затем решают систему (9.445), в результате чего находят распределение циркуляции Г по ячейкам крыла. [36]
Соответствующий анализ показывает, что постоянная по всему размаху скорость скоса, вызванная вихрями, получается в случае распределения циркуляции по размаху по закону полуэллипса. Такое распределение циркуляции получается при эллиптической ( в плане) форме крыльев одинакового профиля и одинаковых углов установки. [37]
В уравнениях (2.6.67) и (2.6.68) в круглых скобках выбран знак плюс, так как рассматриваются симметричные движения, при которых распределение циркуляции по размаху будет также симметричным. [38]
Из доказанного только что свойства одинаковости угла скоса вдоль размаха крыла с эллиптическим распределением циркуляции следует, что геометрически незакрученное крыло с эллиптическим распределением циркуляции будет и аэродинамически незакрученным. [39]
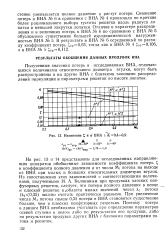 |
Изменение. и т ВНА с 0 4 - 0 5. [40] |
Полученные значения потерь в исследованных ВНА, отличающихся величинами относительного диаметра втулки, могут быть распространены и на другие ВНА с близкими законами распределений циркуляции и параметрами решеток по высоте лопаток. [41]
Таким образом, можно формулировать следующий результат: волновое сопротивление тела вращения при продольном его обтекании может вычисляться по формулам индуктивного сопротивления крыла конечного размаха, если вместо распределения циркуляции по размаху задавать распределение мощности источников по оси тела вращения. [42]
Итак, при принятых условиях геометрической незакрученности и одинаковости аэродинамических характеристик вдоль размаха, крыло с эллиптическим распределением циркуляции будет иметь и эллиптическую форму в плане, подобную кривой распределения циркуляции; такое крыло может быть названо эллиптическим. [43]
Если подъемную силу, как-либо меняющуюся вдоль размаха крыла, и циркуляцию представить в виде как бы связки вихревых нитей внутри крыла, причем плотность этой связки пропорциональна циркуляции, то при ступенчатом распределении циркуляции с задней кромки крыла будут сбегать вихри так, как это изображено на фиг. [44]
На постулате Жуковского-Чаплыгина основываются существующие математические методы определения циркуляции, а следовательно, и подъемной силы как для единичного профиля, так и для решетки профилей; с помощью этих методов удается найти и распределение циркуляции и подъемной силы по размаху крьпа. Эти методы составляют содержание теоретической аэродинамики крыла и решетки крыльев, основные результаты которой излагаются ниже. [45]
Страницы: 1 2 3 4