Распределение - число - частица
Cтраница 1
Распределение числа частиц по высотам предполагает изменение концентраций и микроструктуры аэрозоля с высотой для солевого, пылевого и мелкодисперсного континентального аэрозоля. Вертикальный профиль концентраций различных фракций аэрозоля описывается экспоненциальным соотношением, шкала высот h в котором зависит от высоты г. В табл. 4.12 приведены шкалы высот hc и hm для трех диапазонов размеров частиц континентального и морского аэрозоля соответственно на различных высотах над уровнем моря. [1]
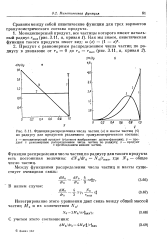 |
Функции распределения числа частиц ( я и массы частиц ( б по радиусу для продуктов различного гранулометрического состава. [2] |
Функция распределения числа частиц по радиусу для такого продукта есть постоянная величина: dN0 / dr0 N0 / гтак, где N0 - общее число частиц. [3]
Для получения кривой распределения числа частиц по размерам применяют методы отсеивания для частиц с диаметром более 60 а. Декантация и седимен-тационные методы применимы к частицам с диаметром до 1 - 2 ju, а с помощью центрифуги и ультрацентрифуги можно расширить этот предел до 0 01 JJL. Мы не будем здесь обсуждать метод оценки фактора формы, предложенный Гейвудом. [4]
 |
Зависимость диэлектрической проницаемости смеси е от объемного содержания непроводящих включений б.| Зависимость кажущейся диэлектрической проницаемости ЕК от межэлектродпого расстояния I. [5] |
По микрофотографиям было вычислено распределение числа частиц по размерам. [6]
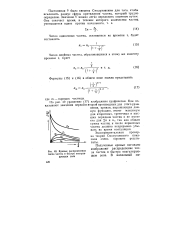 |
Кривые распределения числа частиц в быстро коагулирующем золе. [7] |
Полученные кривые наглядно изображают распределение числа частиц в быстро коагулирующем золе. [8]
Такой вид kf обусловлен маковелловским распределением числа частиц - Bj kT) по кинетической энергии г их поступательного движения. [9]
В [297] модель морского аэрозоля описывает распределение числа частиц по размерам как функцию скорости ветра vy относительной влажности /, высоты z над уровнем моря до 5 км, дальности видимости 5М на уровне моря. [10]
В нек-рых случаях удается определить также дифференциальную ф-цию распределения числа частиц ( их объема, массы, доли частиц или пор) по размерам. [11]
Уравнение (4.38) отображает общи и закон Больцмана и дает распределение числа частиц в зависимости от их потенциальной энергии. [12]
При теоретическом рассмотрении процесса кинематической коагуляции исходят из функции распределения числа частиц по их массе f ( m, т), характеризующей начальное состояние полидисперсной системы капель. [13]
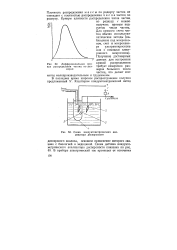 |
Дифференциальная кривая распределения частиц по размерам.| Схема кондуктометрического анализатора дисперсности. [14] |
Плотность распределения массы по радиусу частиц не совпадает с плотностью распределения числа частиц по радиусу. [15]
Страницы: 1 2 3 4