Распределение - число - частица
Cтраница 2
Дальнейшее увеличение числа ступеней уже не приводит к существенному изменению характера распределения числа частиц по времени пребывания. Максимум на кривых плотности распределения вероятностей с увеличением п сдвигается вправо. [16]
Как следует из полученных результатов, при достаточно больших скоростях взвешивающего потока распределение числа частиц в единице объема по высоте будет неоднородным по всей протяженности слоя. [17]
Полученные результаты показывают, что при больших и малых скоростях взвешивающего потока распределение числа частиц по высоте в кипящем слое оказывается весьма различным по своей структуре. Поскольку технологические процессы ведутся обычно при небольших скоростях взвешивающего потока, то в дальнейшем будут рассматриваться только такие режимы, при которых существует область однородного состояния кипящего слоя. [18]
Ромашов [123] приводит численные и графические свидетельства большой согласованности эмпирических данных по распределению числа частиц пыли различных размеров, витающей в воздухе производственных помещений, с вычисленными по его формулам. [19]
 |
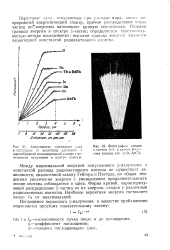
Схема распределения частиц в сечении фонтанирующего слоя по скоростям. [20] |
С целью изучения как пространственного распределения частиц с различными скоростями, так и распределения числа частиц по скорости была применена фотосъемка при различных выдержках. [21]
Используя уравнение ( V - 40), Перрен на основании экспериментального изучения распределения числа частиц по высоте в суспензиях гуммигута рассчитывал значение числа Авогадро; и в этом случае найденное им значение NA 6 7 - 1023 близко к современному. [22]
Исходя из сформулированных выше условий, можно ожидать, что закону Пуассона будет подчиняться распределение числа частиц при радиоактивном распаде, измеряемое в те или иные промежутки времени, если полупериод распада вещества достаточно велик и при распаде не образуются дочерние вещества, испускающие те же частицы. [23]
Первичные лучи, испускаемые при распаде ядра, имеют непрерывный энергетический спектр, причем распределение числа частиц по энергиям напоминает кривую вероятности. Нижняя граница энергии в спектре [ 3-частиц определяется чувствительностью метода исследования; верхняя граница энергии является характерной константой радиоактивного изотопа. [25]
Подставляя в (5.73) конкретное ядро, получим систему дифференциальных уравнений, предназначенных для определения моментов распределения числа частиц по размерам. [26]
При анализе процессов, протекающих в химической аппаратуре с кипящим слоем, большое значение имеет знание характера распределения числа частиц в единице объема в области, занимаемой слоем. Качественный характер такого распределения описывался многими исследователями, однако число работ, содержащих количественные данные указанного типа, сравнительно невелико. [27]
Что касается температурной зависимости интенсивности того или иного вида люминесцентного излучения, то она следует из формулы, выражающей распределение числа частиц по энергетическим уровням в зависимости от температуры. Следует отметить, что поскольку большинство частиц в начале находилось в основном состоянии, то уменьшение их числа с увеличением температуры составляет малую долю от общего числа частиц в состоянии Ег. Следовательно, уменьшение интенсивности стоксова излучения с увеличением температуры будет слабым. Этого нельзя сказать относительно изменения ( увеличения) интенсивности антистоксова излучения. При достаточно высокой температуре люминесцирующей системы общая интенсивность излучения ослабевает. [28]
Кроме средней весовой концентрации, выраженной массой в единице объема, следует отметить такие важные характеристики для городской атмосферы, как распределение числа частиц по размерам и объему. В то же время количество частиц в этой области очень велико в сравнении с остальной частью пробы. Частицы именно этой области размеров обладают способностью проникать в легкие. [29]
Помимо рассмотренных кривых распределения массы частиц по размерам f ( r) d ( m / mmax) / dr иногда используют и иные ( перенормированные) распределения, например дифференциальное распределение числа частиц о 1 по их размерам fjv ( r) d ( o / oVmaiO / dr и дифференциальное распределение поверхности частиц S по их размерам / s ( r) d ( S / Smait) / dr, где е / У таж - общее число частиц, 5та - их общая поверхность. [30]
Страницы: 1 2 3 4