Распределение - гаусс
Cтраница 1
Распределение Гаусса предполагает хаотическое движение молекул, что недопустимо в случае реальных полимерных цепей с фиксированными углами между связями и взаимосвязанным расположением элементарных звеньев. Но это не значит, что в реальной цепи положение первого звена строго определяет положение / - того звена. Иначе, в каждой цепи можно определить звенья, положение которых не зависит от положения первого звена, а также и других звеньев, находящихся на определенном расстоянии от данного t - того звена. [1]
Распределение Гаусса предполагает хаотическое движение молекул, что недопустимо в случае реальных полимерных цепей с фиксированными углами между связями и взаимосвязанным расположением элементарных звеньев. Но это не значит, что в реальной цепи положение первого звена строго определяет положение i-того звена. Иначе, в каждой цепи можно определить звенья, положение которых не зависит от положения первого звена, а также и других звеньев, находящихся на определенном расстоянии от данного i-того звена. [2]
Распределение Гаусса является предельным случаем распределения Пуассона и многих других законов распределения. [3]
Распределение Гаусса определено выражением ( ср. [4]
Это распределение Гаусса, центральная точка y0eat которого быстро удаляется от неустойчивой точки, а ширина ( e2af - I) 1 2 быстро возрастает. [5]
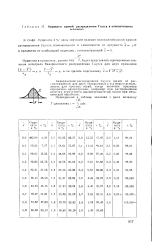 |
Ординаты кривой распределения Гаусса в относительных. [6] |
Ви вариантное распределение Гаусса ( далее не рассматриваемое) для двух независимых хну можно использовать для простых серий, когда значение признака ограничено односторонне, например при распределении величин некруглости ( эксцентрицитетов) валов при механической обработке. [7]
Обобщить распределение Гаусса элементов цепной дроби, перенеся его на трехгранные ( общие. Доказать многомерное обобщение теоремы Лагранжа о периодичности цепных дробей в этой ситуации: топологическая периодичность имеет место, если и только если плоскости - собственные для сохраняющего решетку оператора. В двумерном случае 1-звезды определяют целочисленные углы граничной ломаной, которые, вместе с целочисленными длинами ребер, и составляют элементы цепной дроби. [8]
При распределении Гаусса ст шдартное отклонение а может быть оценено также исходя из величины диапазона. [9]
Интеграл от распределения Гаусса в конечных пределах не берется, но он широко представлен в справочных таблицах. [10]
Это - распределение Гаусса, средняя точка х - vxt которого равномерно перемещается со временем. [11]
Так как распределение Гаусса или распределение, составленное из нескольких ( смешанное) распределений, встречается наиболее часто, то вначале устанавливают, к какому типу ( простому или смешанному) относится полученное распределение. [12]
Это есть распределение Гаусса. [13]
Следовательно, распределение Гаусса полностью определяется средними значениями переменных it их матрицей ковариаций. В частности, если переменные некоррели-рованы, матрица А 1 диагональна, но тогда и А также диаго нальна; следовательно, переменные независимы. Эта независимость всегда может быть получена с помощью линейного и даже ортогонального преобразования переменных. [14]
Гамма-распределения и распределения Гаусса не однопараметрические, как распределения Пуассона, а двухпараметрические, к тому же непрерывные. Возникает необходимость определения второго параметра - дисперсии Dnr и среднеквадратиче-ского отклонения апг. [15]
Страницы: 1 2 3 4