Большая Энциклопедия Нефти и Газа

Никому не поставить нас на колени! Мы лежали, и будем лежать! Законы Мерфи (еще...)

Распределение - гаусс

Cтраница 2

Кривая распределения Гаусса ( по оси ординат отложены значения измеряемой величины N, по оси абс-цисс - вероятная ошибка отдельного измерения р. N - среднее арифметическое значение измеряемой величины.  [16]

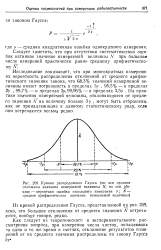
Из кривой распределения Гаусса, представленной на рис. 209, ясно, что большие отклонения от среднего значения N встречаются, вообще говоря, редко.  [17]

Эта функция распределения Гаусса симметрична относительно истинной величины т, которая выбрана здесь в качестве начала для х, что означает равновероятность как положительных, так и отрицательных ошибок.  [18]

Характеристическая функция распределения Гаусса имеет.  [19]

Эта функция распределения Гаусса симметрична относительно истинной величины т, которая выбрана здесь в качестве начала для х, что означает равновероятность как положительных, так и отрицательных ошибок.  [20]

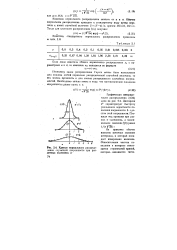Кривые нормального распределения случайной погрешности при различных значениях а.  [21]

Поскольку закон распределения Гаусса может быть использован для анализа любой нормально распределенной случайной величины, то его можно применить и для закона распределения случайных погрешностей.  [22]

Широкое применение распределения Гаусса в статистике основано на доказанном в теории вероятностей утверждении, что случайная величина, являющаяся суммой большого числа независимых случайных величин с конечными дисперсиями и с практически произвольными законами распределения, распределена нормально.  [23]

Точка 100 % распределения Гаусса теоретически соответствует точке, лежащей в бесконечности. Поэтому на сетке она не изображается.  [24]

Постоянные последовательного контроля.  [25]

Предпосылкой является свойство распределения Гаусса, по которому можно оценить среднее квадратическое, исходя из предыдущих исследований. Но в этом случае формулы для вычислений h становятся более сложными.  [26]

Роль нормального закона распределения Гаусса для двумерных случайных величин так же велика, как и для рассмотренных ранее одномерных случайных величин.  [27]

Обычно в справочниках распределения Гаусса, Лапласа и равномерное рассматриваются как разные распределения, хотя в излагаемой здесь концепции - это одно и тоже распределение.  [28]

В сравнении с распределением Гаусса эта теорема дает очень грубое приближение. Но зато она удобна в применении, поскольку позволяет сделать это быстро, не прибегая к обращению к сложным таблицам.  [29]

Заметим, что для распределения Гаусса отсутствие корреляции равносильно независимости.  [30]

Страницы:      1    2    3    4