Биноминальное распределение

Cтраница 1

Биноминальное распределение можно использовать для расчета вероятностей при условиях, когда: ( i) имеется только два возможных исхода в пробе ( например, благоприятный исход или неблагоприятный исход); ( И) независящие друг от друга пробы повторяются некоторое число раз ( п); ( Hi) вероятность благоприятного исхода ( р) неизменна в каждой пробе. [1]

Биноминальное распределение, как мы видели, позволяет, в частности, установить, какое число появлений события А наиболее вероятно. [2]

Биноминальное распределение имеет два параметра 9 и п, причем обычно свободным остается один параметр 6, другой параметр определяется самой задачей. [3]

Биноминальное распределение было получено Я. [4]

Биноминальное распределение, как мы видели, позволяет, в частности, установить, какое число появлений события А наиболее вероятно. [5]

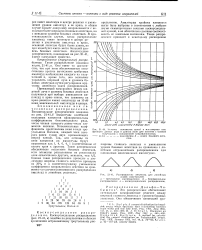Угловое положение нулей и максимумов как функция длины ряда в длинах волн для антенны с осевым. [6]

Биноминальное распределение показано на рис. 21 - 41 6 Амплитуды колебаний отдельных элементов пропорциональны коэффициентам биноминального ряда, число членов которого равно числу элементов антенны. [7]

Форма биноминального распределения зависит от величины его параметров. [8]

Для биноминального распределения существует два типа таблиц. [9]

Формула биноминального распределения вероятностей оказывается весьма неудобной в тех случаях, когда число испытаний достаточно велико. Трудности, связанные с вычислением факториалов больших чисел, делают формулу практически не применимой. [10]

Закон Пуассона выражает биноминальное распределение при большом числе опытов и малой вероятности события. Этот закон называют законом редких явлений. [11]

Для 9 0 5 биноминальное распределение симметрично. При увеличении п и заданном значении 9 биноминальное распределение сходится к нормальному распределению. Если при п - оо одновременно 6 - 0, то биноминальное распределение сходится к распределению Пуассона. [12]

Результаты кратковременных измерений фотоэлектрического счета р ( гг, ., t Т для лазерного луча ( Л и для поляризованного луча от теплового источника с гауссовской статистикой ( Г. ( Приводится из работы Arecchi, 1965. [13]

Это распределение Бернулли или биноминальное распределение по п и его вид имеет естественную интерпретацию. [14]

Это иллюстрирует конкретный пример биноминального распределения. [15]

Страницы: 1 2 3 4