Биноминальное распределение

Cтраница 3

Покажем, что отыскание такого числа может быть выполнено непосредственно без составления полного биноминального распределения. [31]

При малых значениях р или ц вероятности различных значений случайной величины по биноминальному распределению близки к аналогичным вероятностям распределения но Пуассону. [32]

Ширина пика в случае распределения согласно функции Пуассона несколько больше, чем для биноминального распределения. Изменение ширины пика, кроме прочего, зависит от количества пробы, введенной в колонку. Дело в том, что в большинстве случаев на колонку подают больший объем пробы, чем может вместить одна теоретическая тарелка. Поэтому часть пробы, не поместившаяся в первой тарелке, проходит на следующие, и следовательно, хроматографический процесс разделения начинается одновременно на нескольких тарелках. Таким образом, на выходе из колонки фиксируется пик, который является результатом сложения взаимно перекрывающихся хроматографических кривых, соответствующих отдельным начальным тарелкам. Ширина пика возрастает с увеличением пробы. [33]

Покажем, что отыскание та кого числа может быть выполнено непосредственно без составления полного биноминального распределения. [34]

В теории вероятностей известно много законов распределения случайных величин: нормальный закон, распределение Максвелла, биноминальное распределение, показательное распределение, гамма-распределение, распределение Пуассона и др. Существование сравнительно большого числа законов распределения объясняется богатством и многообразием природных явлений. В принципе тот или иной физический процесс, на исход которого злияют случайные факторы описывается одним законом распределения. Однако функции распределения, устанавливающие математическую связь между случайной величиной и вероятностью, могут изменяться за счет изменения условий проведения процесса. При этом изменение интегральной и дифференциальной функций распределения, их трансформация осуществляется за счет изменения постоянных коэффициентов, входящих в математические выражения этих функций. Эти постоянные коэффициенты наз ывают параметрами распределения. [35]

В технологии машиностроения наиболее часто встречаются вероятностно-статистические модели, описываемые следующими законами распределения: закон Бернулли ( биноминальное распределение), закон нормального распределения ( закон Гаусса), закон Пуассона, закон равной вероятности, закон Симпсона и многие другие и их комбинации. [36]

Чтобы учесть в теории такое вырождение дефектов, необходимо предпринять существенный предварительный шаг - построение теории на основе биноминального распределения, которое не ограничивается бесконечным числом событий. Недавно Годин и Мэлой 15, принимая биноминальное распределение, вывели функцию распределения осколков по размерам при одноразовом разрушении. В оригинальной форме их модель не может учесть влияния поверхностных и объемных дефектов, на фактическое существование которых указывают эксперименты. Следует - упомянуть, что результаты Година и Мэлоя отличаются от выводов Мэннинга 34, который ранее рассматривал ту же самую математическую задачу другим методом. [37]

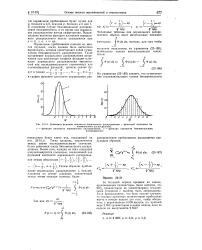Сравнение функции плотности нормального распределения с функцией плотности биноминального распределения. [38]

Нормальное приближение полезно во многих случаях, когда должна быть вычислена вероятность, которая представляет собой сумму членов биноминального распределения. [39]

При сомнении относительно нормальности распределения х / n правильнее определять границы регулирования для q и nq карт по формуле биноминального распределения. Она с большей точностью отражает особенности фактического распределения этой величины. Вероятность того, что в каждой выборке из n изделий число дефектных изделий будет не более d, является вероятностью нормального ( налаженного) хода производственного процесса ( 1 - а), где а - допустимая вероятность возникновения нарушений технологического процесса. [40]

Во многих случаях имеет смысл контроль за устойчивостью количественного анализа осуществлять при помощи некоторого качественного признака, и тогда для статистических оценок нужно пользоваться биноминальным распределением. Например, если текущие анализы в лаборатории выполняются из двух параллельных определений, то в качестве такого признака можно взять число тех анализов, которые пришлось переделывать из-за большого расхождения в параллельных определениях. Допустим, что в результате длительного наблюдения установлен средний процент h % - 7 % бракуемых параллельных определений. Тогда текущий контроль за устойчивостью аналитического процесса можно вести, проверяя число забракованных анализов на каждые 150 выполненных анализов. При п 150, 6 0 07 биноминальное распределение, как это следует из (5.16), может быть представлено нормальным распределением. [41]

Кроме перечисленных распределений, могут быть использованы распределение равномерной плотности; нормальное логарифмическое; гамма-распределение и др. Однако на практике наиболее часто применяют экспоненциальное, Вейбулла, нормальное и биноминальное распределения. [42]

Однако расчет вероятностей по Пуассон1, проще и имеются готовые таблицы таких вероятностей, поэтому во многих сл) чаях при очень малых значениях р или q заменяют биноминальное распределение распределением по Пуассону. Закон распределения по Пуассону в связи с изложенным часто называют законом редких явлений. [43]

Если небольшие боковые лепестки допустимы, то выгоднее использовать распределение по биноминальному закону более высокой степени с отброшенными малыми крайними коэффициентами, Например [5], решетка из восьми диполей при обычном биноминальном распределении имеет ширину диаграммы направленности 31 и КНД 4 8 по сравнению с 17 5 и 8 0 для равномерного распределения; если же взять восемь центральных членов в биноминальном распределении для Л / 15, то получится ширина диаграммы направленности 23, усиление 6 7 и боковые лепестки с уровнем, не превосходящим 27 дб. [44]

Во многих технических задачах возникает вопрос относительно вероятности появления события Л точно г раз, если испытание повторяется и раз, где п г. Если результаты каждого испытания независимы, то эта вероятность дается биноминальным распределением. [45]

Страницы: 1 2 3 4