Пространственное распределение - поля
Cтраница 1
Пространственное распределение полей анализируется с помощью теории Фурье, в которой вместо упомянутого выше временного применяется пространственное преобразование Фурье. С помощью такой операции выводятся интегральные уравнения, которые описывают электромагнитное поле в точке пространства в виде суперпозиции интегралов по поверхности, окружающей данную точку. Тем самым локальный характер уравнений Максвелла заменяется влиянием удаленного поля. Далее будет проведено теоретическое описание дифракции в системе, состоящей из двух таких областей в пространстве: в одной из них имеется излучение, а в другой расположен объект, на котором поле рассеивается или дифрагирует. Интегральные уравнения для обеих областей сшиваются с помощью граничных условий для электромагнитного поля. [1]
Вообще же пространственное распределение полей внутри и вне полости концентрического и плоского резонаторов существенно различно. [2]
Ниже рассмотрим спектральное и пространственное распределения полей нисходящего и восходящего излучений в условиях замутненной атмосферы и влияние атмосферного аэрозоля на лучистый теплообмен, основываясь на данных расчетов, выполненных Н. И. Москаленко, В. Ф. Терзи, А. Р. Закировой с детальным учетом поглощающих и рассеивающих свойств атмосферы. [3]
Наряду с анализом пространственного распределения полей и интенсивностей лазерного локационного сигнала для извлечения информации об объекте представляет интерес и временной анализ амплитуды или интенсивности рассеянного излучения. Наиболее простые представления об использовании временного анализа сигнала относятся к случаю локации цели импульсным излучением с длительностью импульса, сравнимой или меньшей протяженности цели в направлении зондирования. При этом интенсивность / ( t) принимаемого сигнала в каждый момент времени определяется рассеянием от слоя объекта, протяженность которого равна половине протяженности импульса. [4]
Поверхностная волна может существенно влиять на пространственное распределение индуцированных полей и токов. Амплитуда поверхностной волны максимальна на расстоянии порядка длины волны от фронта пучка, где она даже может превосходить амплитуду его собственного поля, и экспоненциально затухает на диффузионной длине / - UTS. Большая амплитуда поля поверхностной волны определяется относительно высокой плотностью поверхностного тока. Дело в том, что на поверхность цилиндра выталкивается заряд порядка заряда пучка, который распространяется со скоростью волны, совпадающей со скоростью пучка. В то же время эффективная толщина поверхностного слоя, где течет этот ток, меньше толщины пучка. Благодаря низкой частоте поверхностной волны индуцируемые ею поля и токи существенно воздействуют на формирование квазистационарного обратного тока в плазме. Значение и направление тока, индуцируемого в поверхностной волне, осциллируют с частотой волны. Поэтому, когда в области максимума амплитуды направление поверхностного тока совпадает с направлением движения электронов, возможно даже усиление тока пучка и сопутствующих ему полей. Наоборот, там, где направление поверхностного тока противоположно току пучка, поверхностная волна усиливает обратный ток и связанное с ним магнитное поле. В этом случае имеет место эффект перекомпенсации пучка. Электроны в зависимости от знака индуцированного магнитного поля будут прижиматься к оси пучка или отталкиваться от нее. Если время нарастания переднего фронта пучка существенно превышает период поверхностной волны, то воздействие волны на плазму, усредненное по периоду осцилляции, будет определяться только этой неосциллирующей частью поверхностного обратного тока. [5]
При любой частоте со волоконный световод может иметь конечное число направляемых мод, пространственные распределения полей Е ( г, со) которых являются решениями волнового уравнения (2.1.18) при соответствующих граничных условиях. Кроме того, световод может иметь континуум ( счетное число) ненаправляемых излучатель-ных мод. [6]
При любой частоте со волоконный световод может иметь конечное число направляемых мод, пространственные распределения полей Е ( г со) которых являются решениями волнового уравнения (2.1.18) при соответствующих граничных условиях. Кроме того, световод может иметь континуум ( счетное число) ненаправляемых излучатель-ных мод. [7]
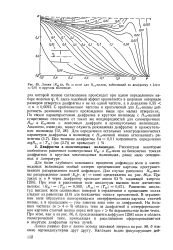 |
Линии Ru ( к, 6 const для Я11 - волны, набегающей на диафрагму с / / а 0 01 в круглом волноводе. [8] |
Для более глубокого понимания процессов дифракции волн в многомодовых волноводах особый интерес представляют картины пространственного распределения полей дифракции. Равенство амплитуд высших волн одинаковых номеров в отраженном и прошедшем полях следует из равенства (3.6) для бесконечно тонких препятствий. В отраженном поле образуется повторяющаяся интерференционная картина стоячей волны, а в прошедшем - уже заметна зона тени за диафрагмой. На больших частотах ( х 4 - f - 5) область тени за диафрагмой и интерференционная картина стоячей волны перед ней при г Qa выражены еще более четко. При этом, как и на рис. 86, б, прослеживается диффузия [258] поля в область геометрической тени, приводящая к расплыванию сформировавшегося в апертуре диафрагмы пучка лучей. [9]
Поэтому при более строгом подходе на рис. 223 необходимо было бы принять во внимание не только пространственное распределение полей, но и фазы изменения напряженностей. [10]
Пространственное распределение поля суммарной частоты можно найти, решая уравнения Максвелла, содержащие Es при заданном пространственном распределении полей накачки и инфракрасного излучения ( приближение заданного поля, см. гл. [11]
 |
Температурные зависимости константы фазового равновесия для водных растворов диоксида углерода ( а азота, воздуха и метана ( б 1 - азот, 2 - воздух, 3 - метан. [12] |
Система уравнений (4.2.1) относится к классу так называемых простых моделей климата и, очевидно, лишь в грубом приближении может описывать климатические изменения, так как не учитывает пространственное распределение полей температуры и влажности. [13]
Рассмотренные методы измерения расхода, использующие линейные индукторы с бегущим или пульсирующим магнитным полем, позволяют получить рассчитываемые градуировочные характеристики. Но получение таких пространственных распределений полей связано с определенными трудностями. [14]
При изложении результатов по каждой конкретной структуре авторы стремились выбрать такой объем графической информации и представить ее в такой форме, чтобы обеспечить переход от количественных характеристик к качественным обобщениям и выводам, что обычно присуще чисто аналитическим методам исследования волновых процессов в простейших ситуациях. Это достигается широким использованием линейных ( от одного параметра) и двухпараметрических зависимостей изучаемых величин, картин пространственного распределения полей дифракции и линий потока энергии в объеме неоднородности, а также рядом других приемов. Такая многосторонняя информация, на наш взгляд, обеспечивает полноту и глубину исследования, лучшее понимание механизма возникновения какого-либо явления, например практически полного преобразования типов волн. [15]
Страницы: 1 2