Нормальное распределение - вероятность
Cтраница 1
Нормальное распределение вероятности далеко не всегда является хорошей моделью распределения торговых прибылей и убытков. Более того, ни одно из распространенных распределений вероятности не является идеальной моделью. Поэтому мы должны сами создать функцию для моделирования распределения наших торговых прибылей и убытков. [1]
Нормальное распределение вероятностей занимает в теории вероятностей центральное место. Название связано с открытием Гаусса, согласно которому при повторении испытаний полученные значения по этому распределению нормально соответствуют обычному закону ошибок. [2]
Нормальное распределение вероятностей имеет в теории вероятностей большое значение. В частности, оказывается, что закон распределения суммы достаточно большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, близок к нормальному распределению. [3]
Нормальное распределение вероятностей ( normal distribution) - наиболее широко используемое непрерывное распределение вероятностей, обычно имеющее вид колоколобразной кривой и полностью описываемое математическим ожиданием и дисперсией. [4]
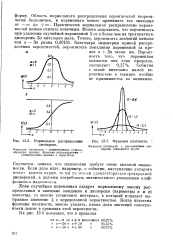 |
Нормальное распределение [ IMAGE ] - 7. Функция плотности. [5] |
Область нормального распределения вероятностей теоретически бесконечна, и переменная может принимать все значения от - оо до оо. [6]
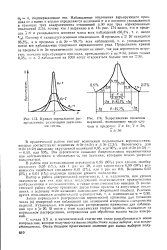 |
Кривая нормального рас - [ IMAGE ] Теоретические полигоны. [7] |
Закон нормального распределения вероятностей применим для большого числа ( п) измерений или наблюдений так называемой генеральной совокупности явлений. В связи с этим классическая теория ошибок, основанная на нормальном распределении, неприменима для обработки малого числа измерений. [8]
Закон нормального распределения вероятностей широко используется в процессе анализа рисков финансовых операций. Его важнейшие свойства, такие, как симметричность распределения относительно средней, ничтожно малая вероятность больших отклонений значений случайной величины от центра ее распределения, правило трех сигм, позволяют существенно упростить проведение анализа и выполнение сопутствующих расчетов. [9]
Разумеется, нормальное распределение вероятностей является математической моделью, к которой распределение реальных случайных процессов может приближаться более или менее точно. [10]
При изучении нормальных распределений вероятности очень удобно использовать характеристические функции. [11]
Если случайная величина имеет нормальное распределение вероятностей, то, как известно ( см., напр. [12]
Вся площадь под кривой нормального распределения вероятностей принимается за единицу. [13]
Выше мы установили, что нормальное распределение вероятностей является предельным для нормированных средних или, что то же самое, для нормированных сумм одинаково распределенных слагаемых. [14]
В общем же случае рассматриваемые многомерные нормальные распределения вероятностей могут оказаться и вырожденными, и поэтому их удобнее задавать не плотностями вероятности, а соответствующими многомерными характеристическими функциями или даже характеристическим функционалом. Аккуратное доказательство того, что каждое положительно определенное ядро представляет собой корреляционную функцию некоторой гаус-совской случайной функции X ( t) r может быть найдено ( сразу для общего случая комплексных функций X ( 0), например, в [ 83, гл. Среднее значение m ( t) и дисперсия D ( t) пуассоновского процеса X ( t) очевидно равны среднему значению и дисперсии числа пуассоновских точек tk таких, что 0 1& следовательно, m ( t) D ( t) Kt ( ср. [15]
Страницы: 1 2 3 4