Нормированное нормальное распределение

Cтраница 1

Нормированное нормальное распределение позволяет составить таблицу для определения интегральной функции. [1]

Таблица интегральной функции нормированного нормального распределения имеет несколько разновидностей. [2]

Таблица значении плотности вероятностей для нормированного нормального распределения приведена в прил. [3]

У 0 002 мм, плотности нормированного нормального распределения p ( ti) взяты из табл. 5 приложения. Число степеней свободы k8 - 2 - 33, поскольку четыре интервала были объединены в два. [4]

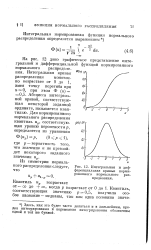
Дифференциальная функция нормированного нормального распределения. [5]

На рис. 3.11 показан график дифференциальной функции нормированного нормального распределения. Кривая может быть использована для любых значений отклонений при условии, что t 1 соответствует А од. [6]

Макс иог, где и - аргумент функции нормированного нормального распределения ( квантиль), соответствующий принятой вероятности, то увеличение этой вероятности с 0 95 до 0 99 означает соответствующее увеличение квантиля, следовательно, оценки значения Макс - Это приводит к возрастанию риска ложной тревоги у изготовителя ( риска оценить хороший продукт как негодный) или к необходимости ужесточить внутренний допуск. То и другое изготовителю не всегда выгодно экономически, но может оказаться необходимым при выпуске продукции ответственного назначения или дорогостоящей и в тому подобных ситуациях. [7]

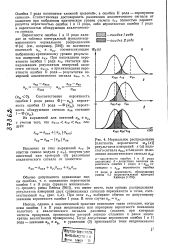
Интегральная и дифференциальная кривые нормированного нормального распределения. [8]

На рис. 12 дано графическое представление интегральной и дифференциальной функций нормированного нормального распределения. Абсцисса интегральной кривой, соответствующая некоторой заданной ординате, называется кван-тилью. [9]

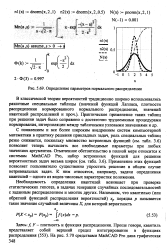
Нормальное распределение [ плотность вероятности wa ( x ] результатов измерений х ( а холостого сигнала аХол и близкого по величине аналитического сигнала аан. [10]

Вероятности ошибок I и II рода находят из таблицы интегральной функции нормированного нормального распределения Ф ( и) ( см., например, [549]) по значениям квантилей upt и ир. [11]

Поскольку здесь N, N2, то / i e / 2 совпадают с квантилями нормированного нормального распределения. [12]

Допустимые значения, основанные на коэффициентах вариации генеральной совокупности и выборки. [13]

К ] - с, ( 1 - д) и ( 1-с) - процентные квантили нормированного нормального распределения. Таким образом, анализ допустимых значений, основанный на статистиках генеральной совокупности, показывает слабую их чувствительность к объему выборки. [14]

Определение параметров нормального распределения. [15]

Страницы: 1 2