Экстремальное распределение

Cтраница 2

XX U), которым соответствуют положительные вероятности Р ( х, и) 0 в экстремальном распределении. Производная от (9.4.5) по Р ( х, и) должна обращаться в нуль. [16]

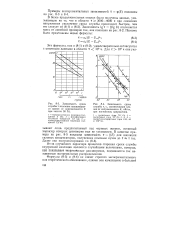
Функция распределения элегазовой изоляции при наличии дефекта, фиксированного на поверхности электрода ( вероятностная сетка нормального. [17]

При весьма большом числе частиц, как и в слабонеоднородном поле без частиц, следует вести расчеты с экстремальным распределением. [18]

Зависимость срока службы т изоляции вращающихся машин от напряженности Е при частоте 50 Гц.| Зависимость срока службы т, с, синтетических пленок от напряженности Е, кВ / см, при постоянном напряжении. [19]

Из-за случайного характера процессов старения сроки службы внутренней изоляции являются случайными величинами, которые, КИК показывает теоретическое рассмотрение, подчиняются так называемым экстремальным распределениям. [20]

Поэтому при рассмотрении вопроса об экстремальном распределении температур по каскадам, соответствующем минимуму массы всего устройства, включая тепловой радиатор, будем приближенно полагать, что все каскады работают в режиме максимального холодильного коэффициента. [21]

Предполагается, что это распределение существует и единственно. То подмножество из Y, элементы которого имеют ненулевые вероятности в экстремальном распределении, обозначим Y и будем называть активным множеством. [22]

При достаточно малых Р ( у ( когда - In Р ( г / а) - рс ( yj - у О ( Р ( г / i)) 0) выражение в правой части (3.3.9) будет заведомо положительным. Следовательно, энтропия распределения Р, удовлетворяющего тем же условиям (3.3.8), будет превосходить энтропию экстремального распределения Р0, что невозможно. Значит, элемента ylt имеющего в экстремальном распределении нулевую вероятность, не должно быть. [23]

Лагранжа, определяемый из нормировочного соотношения. Поскольку в (7.5) вариации 8W уже произвольны, то In Wi 1 - а 0, так что вероятности Wi экстремального распределения не зависят от i. Поскольку же 82а 0 при любых вещественных 8VVt ( в том числе и сохраняющих нормировку), то найденное экстремальное распределение дает максимум энтропии при дополнительном условии нормировки. Но независимость Wi от i означает полную хаотичность ансамбля. Первое требование к энтропии, таким образом, действительно выполнено. [24]

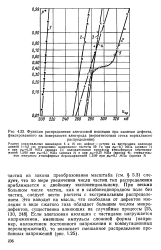
Электрическая прочность. Првзст ( а и разброс YE ( б при аппроксимации электрической прочности промежутка в элегазе при наличии. [25]

Обе группы дефектов часто воссоздаются в лабораториях с целью изучения. Они приводят обычно к снижению - иногда чрезвычайно сильному [25] - пробивных напряжений по сравнению с ненарушенной изоляцией сжатым газом, причем экстремальное распределение больше не может быть использовано. [26]

Рассматривая вопросы, связанные с оценкой риска, аналогично рассуждениям, проведенным в разд. Однако вычислительные затраты, связанные с применением адаптивного критерия, существенно выше. Экстремальные распределения или точки необходимо получать из систем неравенств, которые составляются на основании всей возможной информации о распределении внешних состояний. Риск, сопутствующий принятию решения по адаптивному критерию [22], не оценивается, тогда как использование гибкого критерия (7.1) предусматривает оценку и контроль величины допустимого риска. Гибкий критерий принятия решения (7.1) характеризуется большой степенью общности с классическими критериями - при соответствующей оценке риска е - выбор варианта решения может выполняться, кроме выше описанных случаев, по S-критерию ( разд. Таким образом, область применения данного критерия значительно шире по сравнению с классическими и содержит элементы моделирования процесса с целью улучшения качества решения. [27]

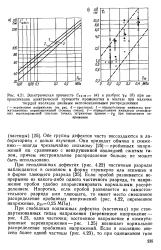
Распределение Вейбулла напряжения пробоя промежутка плоскость - плоскость в трансформаторном масле при различной длительности приложенного переменного напряжения. [28]

Распределение Вейбулла успешно используется как для описания масляных изолирующих промежутков, так и для бумажно-масляной изоляции [260-262], и дает возможность единого описания этого типа изоляции. Поскольку часто масляная изоляция может изучаться лишь на малых моделях, большую роль играет правильность их соотнесения с крупными техническими изделиями ( например, изоляция трансформатора) с помощью закона преобразования масштаба ( см. гл. Экстремальные распределения и в этом случае раскрывают благоприятные перспективы. [29]

Особый интерес представляют экстремальные распределения вероятностей, соответствующие максимуму информационной энтропии при дополнительном условии, что некоторые случайные величины Ат ( г) имеют заданные средние значения. В теории информации такие распределения часто называются наиболее объективными, так как они не содержат дополнительной информации, которая не следует из имеющихся данных. Как мы скоро увидим, экстремальные распределения играют важную роль и в статистической механике. Поэтому имеет смысл кратко обсудить способ построения распределений этого типа. [30]

Страницы: 1 2 3