Экстремальное распределение

Cтраница 3

При достаточно малых Р ( у ( когда - In Р ( г / а) - рс ( yj - у О ( Р ( г / i)) 0) выражение в правой части (3.3.9) будет заведомо положительным. Следовательно, энтропия распределения Р, удовлетворяющего тем же условиям (3.3.8), будет превосходить энтропию экстремального распределения Р0, что невозможно. Значит, элемента ylt имеющего в экстремальном распределении нулевую вероятность, не должно быть. [31]

Мы показали, что распределение вероятностей (1.3.21) соответствует экстремуму информационной энтропии. Проверим, является ли этот экстремум максимумом. Рассмотрим два нормированных распределения wi и г, первое из которых - экстремальное распределение, а второе - некоторое другое нормированное распределение, соответствующее тем же значениям средних ( Лт), а в остальном произвольное. [32]

В конфокальном резонаторе фаза не меняется по зеркалу, а само поле ( для реальных чисел N) концентрируется вблизи оси. Плоский резонатор, напротив, характеризуется максимальным изменением фазы и наиболее широким распределением амплитуды. Для резонаторов промежуточных конфигураций распределения амплитуды и фазы постепенно изменяются, переходя от одного экстремального распределения к другому. [33]

Лагранжа, определяемый из нормировочного соотношения. Поскольку в (7.5) вариации 8W уже произвольны, то In Wi 1 - а 0, так что вероятности Wi экстремального распределения не зависят от i. Поскольку же 82а 0 при любых вещественных 8VVt ( в том числе и сохраняющих нормировку), то найденное экстремальное распределение дает максимум энтропии при дополнительном условии нормировки. Но независимость Wi от i означает полную хаотичность ансамбля. Первое требование к энтропии, таким образом, действительно выполнено. [34]

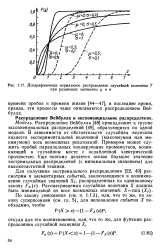Логарифмически нормальное распределение случайной величины Y при различных значениях ц и а. [35]

Распределение Вейбулла [48] принадлежит к группе экспоненциальных распределений [49], образующихся по одной модели. В зависимости от обстоятельств случайная величина является экспериментальной величиной ( максимумом или минимумом) всех возможных реализаций. Примером может служить пробой параллельных изолирующих промежутков, возникающий в случайном месте с ослабленной электрической прочностью. Уже поэтому делается ясным большое значение экстремальных распределений ( с минимальным значением) для высокочастотной техники. [36]

Простое часто встречающееся применение этого принципа дает стандартная система экзаменационных оценок А, В, С, D, F. Оставляя в стороне оценку F, обладающую особыми свойствами ( она указывает, что студент должен сдавать экзамен еще раз), можно сделать вывод, что для получения из системы оценок максимального количества информации нужно стремиться к тому, чтобы все остальные оценки встречались одинаково часто. Можно, конечно, повысить значимость самых высоких знаний, ставя сравнительно мало оценок А. При этом, однако, информации придается другой смысл, отличный от определенного выше. Обычная практика американской аспирантуры заключается в том, что ставятся только оценки А и В. Это приводит к напрасной потере пропускной способности системы. Экстремальное распределение, при котором одно из pi равно 1, а все остальные равны 0, соответствует случаю постоянного сигнала. При этом не передается никакой информации. [37]

Страницы: 1 2 3