Получающееся распределение

Cтраница 1

Получающееся распределение изображено в нижней части фиг. А 10 см -, Г 300 К; во внимание принят множитель 2 в выражении для статистического веса при К - - / - - 0 и предположено, что спин ядра очень велик ( или что молекула является симметричным волчком случайно. Кривая в верхней части фиг. J, независимо от значения К. [1]

Проявление астигматизма при щели конечной высоты. [2]

Получающееся распределение освещенности зависит от соотношения между величинами / г и / а. [3]

Поэтому описание получающихся распределений с помощью только средних значений d ( что имеет место в большинстве проведенных работ), является совершенно недостаточным. Значительно более полное представление о распределениях d по величинам я, F и G может быть получено, если к средним значениям дисперсности добавить другие статистические характеристики, отображающие основные свойства этих распределений. [4]

Второй момент получающегося распределения равен сумме вторых моментов двух начальных распределений. [5]

Оказалось, что для резко меняющихся функций получающееся распределение узлов было далеко от оптимального, а в случае функций с разрывами программа не могла вычислить интеграл. [6]

Главный интерес здесь представляют вычисление скорости диффузии электронов по направлению к фронту скачка уплотнения и получающееся распределение электронов. Для рассматриваемого случая степень равновесной ионизации составляет примерно 10 %; следовательно, концентрацией электронов, соответствующей степени ионизации меньше 0 1 %, можно пренебречь. В таком случае остается определить, окажет ли сильное влияние различие Тк и Т для х 10 - 3 на определение скорости диффузии электронов. [7]

Гаусса) совпадает с серединой поля допуска ( являющейся и началом отсчета х), то получающееся распределение остается симметричным ( фиг. [8]

Осевое распределение температур в трубе и гильзовом термокомпенсаторе при трех типичных граничных условиях. [9]

В основном проблема конструирования гильзового термокомпенсатора сводится к обеспечению такого распределения температур по его оси, чтобы получающееся распределение температурных напряжений в гильзе было приемлемым. Несколько интересных случаев рассмотрено на рис. 7.12. Если основным фактором является теплопроводность по оси гильзы, то температура изменяется линейно с изменением осевого положения, как показано на рис. 7.12, а. [10]

Если центр группирования полного рассеивания не совпадает с серединой поля допуска ( до г 0), то получающееся распределение является несимметричным ( фиг. [11]

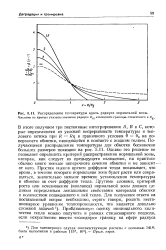Распределение температуры вдоль радиуса нормальной зоны. Числами на кривых указаны значения радиуса Кт холодной границы, отнесенного к К. [12]

В итоге получаем три постоянные интегрирования А, В и С, которые определяются из условий непрерывности температуры и теплового потока при R q и граничного условия 6 Э0 на поверхности обмотки, находящейся в контакте с жидким гелием. Получающееся распределение температуры для обмотки бесконечно больших размеров показано на рис. 5.11. Однако это решение не позволяет определить критерий распространения нормальной зоны, которая, как следует из предыдущего изложения, на практике обычно много меньше поперечного сечения обмотки и не зависит-от него. Простая оценка времен диффузии тепла показывает, что время, в течение которого нормальная зона будет расти или сокращаться, значительно меньше времени установления температуры в обмотке за счет - диффузии тепла. Другими словами, критерий роста или исчезновения ( коллапса) нормальной зоны должен целиком определяться локальными свойствами материала обмотки и количеством подведенного к ней тепла. [13]

Рассчитаны распределения образующихся в результате реакции молекул NO по колебательным состояниям. Было получено, что дисперсия получающихся распределений сильно возрастает с увеличением v - колебательного уровня молекулы N2 и VK - относительной скорости реагентов. При v 8, VR 0 8 106 см / с и v 2, VR 1 0 106 см / с молекулы NO практически равномерно распределены по энергетически возможным колебательным уровням. [14]

Как было нами показано ранее [3], при распылении жидкости вращающимися распылителями в газовую среду нормальной плотности средняя дисперсность капель получающегося рас-пыла d зависит от абсолютной скорости выходящей жидкости и. Поэтому при рассмотрении вопроса о характере получающихся распределений диаметра капель должна быть учтена возможность влияния каждого из вышеуказанных факторов. [15]

Страницы: 1 2