Ограниченное распределение

Cтраница 1

Ограниченное распределение приводит к корректному распределению, необходимому для алгоритма моделирования ансамбля с постоянной температурой. [1]

Ограниченное распределение тока, находящееся во внешнем магнитном поле с вектором индукции В ( х), испытывает действие сил и вращающих моментов, возникающих в соответствии с законами Ампера. [2]

Чтобы ограниченное распределение заряда было устойчиво, необходимы силы неэлектромагнитного характера. Поэтому в рамках уравнений Максвелла и специальной теории относительности следует отказаться от чисто электромагнитной модели материи. Нам известны сильные неэлектромагнитные взаимодействия, существующие в природе. Однако внутренняя структура Частиц в настоящее время остается в основном неизвестной. Единственное исключение представляют нейтрон и протон. Их электромагнитная структура исследовалась с помощью рассеяния электронов высоких энергий, причем электроны рассматривались как точечные частицы и считалось, что законы электродинамики не изменяются на малых расстояниях, характерных для рассматриваемой задачи. [3]

Таким образом, на ограниченное распределение тока в неоднородном магнитном поле действует сила, пропорциональная магнитному моменту этого тока m и определяемая выражением (5.69) В качестве простого приложения полученного результата можно определить среднее по времени значение силы, которая действует на заряженную частицу, движущуюся по спирали в неоднородном магнитном поле. Как известно, заряженная частица в однородном магнитном поле движется по окружности в плоскости, нормальной к полю, сохраняя постоянную скорость в направлении поля; траекторией движения частицы является, таким образом, спираль. [4]

Эти соотношения в случае ограниченных распределений, с которыми приходится иметь дело в практике, дают более высокую надежность вывода. [5]

Q ( X) описывает ограниченное распределение заряда. [6]

Таким образом, в интересующем нас приближении поле ограниченного распределения источников может быть представлено как сумма полей электрического и магнитного диполей и электрического квадруполя. [7]

В § 6 эти общие результаты будут применены к ограниченным распределениям тока. [8]

В этой главе основное внимание уделяется рассмотрению потенциала, обусловленного ограниченным распределением заряда, и дается его представление в виде разложения по мультиполям. В основном разложение проводится по сферическим гармоникам, но для нескольких первых мультиполей обсуждается их представление и в декартовых координатах. Затем вычисляется энергия мультиполя во внешнем электрическом поле. Путем рассмотрения поведения атомов в приложенном внешнем поле в сочетании с подходящей процедурой усреднения выводятся макроскопические уравнения электростатики. Затем описываются свойства диэлектриков, устанавливаются граничные условия для них и решаются некоторые типичные краевые задачи при наличии диэлектриков. На простых классических моделях иллюстрируются основные свойства диэлектриков: поляризуемость и диэлектрическая восприимчивость. В заключение рассматривается вопрос об электростатической энергии при наличии диэлектриков. [9]

В таком случае говорят, что Р ( х) есть непрерывное, однородное и ограниченное распределение. [10]

И таком случае говорят, что Р ( х) есть непрерывное, однородное и ограниченное распределение. [11]

Аналогичным образом, подставляя в (5.13) разложение (5.65), можно найти полный вращающий момент, действующий на ограниченное распределение тока. При этом уже нулевой член разложения оказывается отличным от нуля. [12]

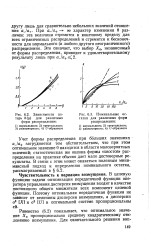Зависимости потерь h ( y для различных форм распределения.| Номинальные остатки для различных форм распределения. [13]

При aja - - схз характер изменения 6 различен: эта величина стремится к конечному пределу для всех ограниченных распределений и стремится к бесконечности для нормального ( и любого другого неограниченного) распределения. [14]

Наличие предела у экспериментальных ошибок, случайных и систематических - хорошо известный каждому экспериментатору факт, означающий, что ошибки подчиняются ограниченному распределению. Практически предельные ошибки измерений могут быть вычислены как сумма модулей приборных ошибок и ошибок, вносимых с поправками к показаниям приборов, и поэтому предполагаются известными экспериментатору. Таким образом, предельные ошибки включают в себя наряду со случайной и систематическую составляющую. [15]

Страницы: 1 2