Инвариантное распределение

Cтраница 1

Инвариантные распределения формально представляют собой не что иное как неподвижные точки этого функционального уравнения. [1]

Инвариантное распределение существует у каждой цепи с конечным числом состояний. [2]

Следовательно, инвариантные распределения здесь совпадают. [3]

Если цепь обладает инвариантным распределением вероятностей & то ft0 для каждого Ek, являющегося либо невозвратным, либо возвратным нулевым состоянием. [4]

Неприводимая апериодическая цепь имеет инвариантное распределение только тогда, когда она является эргоди-ческой. [5]

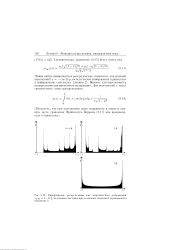Инвариантные распределения для логистического отображения хп 1 - хп, полученные численно при различных значениях управляющего параметра А. [6]

Поэтому для переменной у инвариантное распределение однородное. [7]

В простых случаях вид инвариантного распределения можно найти явно. [8]

Неприводимая непериодичная цепь Маркова обладает инвариантным распределением вероятностей uk ] тогда и только тогда, когда она эргодична. [9]

Следовательно, существует хотя бы одно инвариантное распределение, а когда оно существует, оно является эргодическим. [10]

Мы знаем, что неприводимая цепь обладает инвариантным распределением вероятностей только тогда, когда ее состояния имеют конечные средние времена возвращения. Если состояния цепи возвратные нулевые, то существует инвариантная мера, единственная с точностью до постоянного множителя. При этих обстоятельствах заслуживает внимания тот факт, что преобразование (12.3) определяет стохастическую матрицу Q, если uk является строго положительной инвариантной мерой. В этом смысле каждая строго положительная инвариантная мера определяет обращенную цепь Маркова. [11]

В примере 7, е) мы обнаружили, что инвариантное распределение вероятностей существует только тогда, когда сходится ряд. Инвариантной меры не существует, когда произведение Pi. В этом случае цепь невозвратна. [12]

Таким образом, это есть необходимое и достаточное условие для существования инвариантного распределения вероятностей; если же последнее существует, то оно с необходимостью единственно. [13]

Весьма важным свойством марковской цепи для применений в вычислительной физике является существование инвариантного распределения состояний системы. При применении стохастических методов обычно стартуют с начального состояния х -, чья абсолютная вероятность а также задана изначально. В конце концов состояния распределятся в соответствии с заданным распределением. [14]

Объяснение возникновения сингулярности в инвариантном распределении, порождаемом одномерным отображением с экстремумом. [15]

Страницы: 1 2