Квантовое распределение

Cтраница 2

Книга является практически исчерпывающим введением в современную квантовую оптику и охватывает широкий спектр вопросов, в том числе: неклассические состояния света, методы инженерии и реконструкции квантовых состояний, квантовую томографию, метод ВКБ и фазу Берри, динамику волновых пакетов и интерференцию в фазовом пространстве, квантовые осцилляции Раби, квантовые распределения в фазовом пространстве и методы их измерения, процессы затухания и усиления поля в резонаторах, динамику ионов в ловушках, оптику атомов в квантованных световых полях, квантовое перепутывание как инструмент для квантовых измерений. Оригинальный подход с акцентом на фундаментальную роль пространства фазовых переменных позволяет автору очень наглядно излагать и интерпретировать разнообразные разделы квантовой оптики, облекая книгу в форму, тонко дополняющую другие издания в этой области. [16]

Квантовое распределение Ферми Дирака крайне нечувствительно к температуре. [17]

На рис. 4.2 а показана зависимость ( L2) от номера толчка при k 5, когда классическое фазовое пространство практически полностью хаотично. В течение первых 50 толчков классическое и квантовое распределения вероятнотей близки друг к другу. Однако в дальнейшем квантовая диффузия замедляется, а после 1000 толчков практически останавливается. На этом графике по вертикальной оси отложен логарифм функции распределения fN ( L) после 1000 толчков. [18]

В своей академической книге по теории скрытых переменных ( СП) Белифант показывает, что теории СП не столь далеки от квантовой механики ( КМ), как это может показаться. Рассуждения и наблюдения Белифанта побуждают нас применить теорию квантового распределения к системе спинов 1 / 2, поскольку она в большой степени соответствует квантовой оптике. При этом мы предлагаем теорию скрытых переменных, которая согласуется с квантовой теорией во всем, что касается двухчастичных корреляционных экспериментов, но, очевидно, является нелокальной. [19]

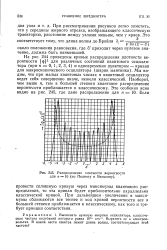Распределение плотности вероятности для п 10 ( по Полингу и Вильсону. [20]

Мы видим, что при малых квантовых числах п квантовый осциллятор ведет себя совершенно иначе, нежели классический. Наоборот, чем выше п, тем в большей степени квантовое распределение вероятности приближается к классическому. [21]

Правда, соответствие это менее выражено, чем в разобранном ранее случае непрерывного распределения энергии. Это является следствием уже обсуждавшейся выше меньшей точности расчета для квантового распределения энергии. Однако и в этом случае можно определить, по крайней мере, порядок величины параметров барьера, поскольку барьеры в обоих случаях оказываются тождественными. [22]

Параметр Месси ( см. § 2) в случае ji - 5 т обычно либо порядка единицы, либо значительно меньше, так что наиболее вероятны столкновения, приводящие к многоквантовым колебательным переходам. Это обстоятельство вместе с сильным неравенством (7.1) позволяет при изучении процесса диссоциации заменить квантовое распределение энергии осциллятора непрерывным. [23]

Обратимся теперь к выводу интеграла столкновений, пригодного для случая газа частиц, находящегося при низких температурах, когда числа заполнения квантовых состояний не малы по сравнению с единицей. Имея в виду соображения, использованные при переходе от формулы (53.7) к (53.8), пренебрежем зависимостью одночастичных квантовых распределений от пространственных координат. [24]

Действующие в молекулах силы притяжения и отталкивания имеют, таким образом, классическую природу, классическое толкование, но, конечно, квантовое распределение электронов выражается в той плотности, которую мы должны приписать для распределения отрицательного заряда внутри общего электронного облака. [25]

Рассмотренная выше теория [51] была первой попыткой априорного расчета относительных скоростей отдельных стадий подвижности протона без использования эмпирических приближений. Эйген и де Майер [93], которые фактически поддержали механизм, предложенный Конуэем, Бокрисом и Линтоном, сделали ряд замечаний относительно этих расчетов. Они рассмотрели вопрос о квантовом распределении и показали, что использование квантового описания энергетических состояний протона, приближающегося к барьеру, не влияет существенно на величину расчетной подвижности - туннельный переход происходит гораздо быстрее, чем структурная реориентация - и не может достаточно обоснованно объяснить изотопный эффект. [26]

Таким образом, разным частотам соответствует различная средняя энергия осциллятора. Однако легко показать, что при малых частотах и высоких температурах квантовое распределение энергии становится малозаметным и формула Планка переходит в классическую формулу закона равномерного распределения. В самом деле, при малом v и большом Т показатель степени в ( 5, 142) становится достаточно малым. [27]

Теперь допустим, что идеальный газ, состоящий из N молекул, находится в состоянии термодинамического равновесия. Применение распределения Гиббса к молекуле газа опять даст распределение (96.1) или (96.3), которое и называется квантовым распределением Больцмана. Имеется существенное различие в применении распределения Больцмана к локализованным слабо взаимодействующим частицам и молекулам идеального газа: для слабовзаимодействующих частиц распределение Больцмана выполняется строго, а для молекул идеального газа это распределение выполняется с известной точностью. [28]

ПШГх, ориентированный под углом 0 к вертикали, а частица 1 со скрытой переменной / 3 пройдет через ПШГ1, ориентиованный под углом 5 к вертикали. Классически эти вероятности, конечно, положительны. Таким образом, интегрирование по этим величинам дает совместную вероятность прохождения Pi2 ( a; ь) - Общий вид Pi2 ( a5 ь) полученный из теории квантовых распределений очень походит на классический ( ср. [29]

Еще одним фазовым распределением, основанным на когерентных состояниях, является Р - распределение. Эта функция была введена одновременно и независимо друг от друга Глаубером ( R.J. Glauber) и Сударшаном ( G. Поэтому мы решили, следуя алфавитному порядку, назвать эту функцию фазовых переменных Р - рас-пределением Глаубера-Сударшана. Из-за этих особенностей квантовых распределений в фазовом пространстве, чуждых для распределения вероятностей, мы называем их распределениями / свази-вероятности. [30]

Страницы: 1 2 3