Частное распределение

Cтраница 3

По основным теоретическим характеристикам ф ( х, у) или F ( х, у) могут быть еще установлены частные распределения и условные распределения двухмерной непрерывной случайной величины. [31]

В этом уравнении г 0 в центре трубы; а, Ъ, с, 0 - постоянные, характерные для частных распределений газосодержания. [32]

Крамере действительно вывел (8.7.1) из (8.7.4), но его Р ( Х, V, t) не вполне совпадает с частным распределением, полученным интегрированием Р ( Х, V, t) по всем V. [33]

Почти очевидно, что мы можем всегда найти бесконечное число распределений в произведении пространств, таких, что для каждого из них частные распределения ( см. параграф 8.4), соответствующие подпространствам Rm и Rn, совпадают с двумя заданными распределениями в этих пространствах. [34]

При проверке гипотезы Я0 по двумерной критической статистике у ( п) ( у ( Y) Для которой известны ( затабулированы) лишь частные распределения ее компонент, мы будем использовать следующие вероятностные соотношения и оценки. [35]

Функция FV ( JCV) определяет некоторое одномерное распределение, которое мы будем называть частным распределением переменной x f Мы можем конкретно представить себе это частное распределение так: предположим, что каждая частица массы в первоначальном л-мерном распределение движется к оси х по прямой перпендикулярной оси х до тех пор, пока не осядет на эту ось. Каждая переменная ху имеет, конечно, свое собственное частное распределение, которое может быть отлично от частных распределений других переменных. [36]

Видно, что в случае независимых переменных ( А4 - - / г2) - й объединенный момент получается как произведение ki-ro и kz-ro моментов соответствующих частных распределений. [37]

Им удалось, в частности, показать, что МБР разветвленного полимера ( ветви которого возникают в результате передачи цепи на полимер) может быть представлено в виде суперпозиции частных распределений для фракций, характеризуемых возрастающими степенями разветвленности. Идея Бамфорда и Томна заключалась в том, что, если сформулировать кинетическую схему, моменты функции распределения ( § 2) могут быть выражены через кинетические параметры, а функция распределения в свою очередь может быть воспроизведена по своим моментам. Однако и эти авторы получили достаточно сложные выражения, не всегда удобные для практического применения. [38]

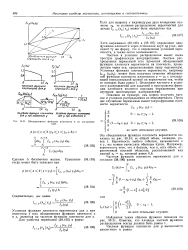Объединенная функция плотности и ее составляющие. [39]

Частное и условное распределения имеют очень простую графическую интерпретацию. Частное распределение переменной есть проекция объединенной функции плотности вероятности на плоскость, проведенную через оси, представляющие нашу переменную. Отыскание частного и условного распределений для заданной в пространстве функции плотности является хорошим упражнением при изучении многомерных распределений. [40]

Графический способ определения корней характеристического уравнения. [41]

Метод разделения переменных позволяет получить совокупность частных решений 9, удовлетворяющих дифференциальному уравнению теплопроводности и граничным условиям. Каждому значению корня ип соответствует частное распределение температуры. [42]

Этот закон зависит от пяти параметров тх, ту, зх, ау и гху. Для выяснения смысла этих параметров определим частные распределения случайных величин системы. [43]

В основе этих двух способов изображения органических молекул лежит реальное явление: если электронная плотность в молекуле может быть распределена несколькими способами, то все эти способы будут осуществляться, так как перераспределение-ведет к выигрышу энергии, к стабилизации молекулы. В таком случае ни одно из возможных частных распределений электронной плотности не может отвечать реальной молекуле. Ей может соответствовать только некая гибридная формула, отражающая все возможности с различными долями вероятности, или набор граничных формул, отражающий все или по крайней мере главные из возможных способов распределения электронной плотности. Использование нескольких граничных формул особенно необходимо, когда два или несколько способов распределения электронной плотности не отличаются или мало отличаются по энергии. [44]

Разложение (22.4.1) показывает, что величины mj и jk, как обычно, играют роль средних значений и центральных моментов второго порядка. Далее, из (22.4.3) следует, что любое частное распределение нормального распределения само нормально. [45]

Страницы: 1 2 3 4