Логарифмическое распределение

Cтраница 2

Кривая 2 отражает логарифмическое распределение осредненной скорости в пристенной турбулентной части пограничного слоя. [16]

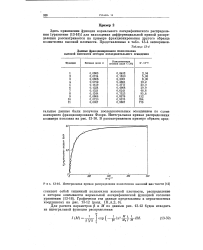Интегральная кривая-распределения полиэтилена высокой плотности. [17]

Здесь применение функции нормального логарифмического распределения [ уравнение ( 13 - 16) ] для нахождения дифференциальной кривой распределения рассматривается на примере фракционирования другого образца полиэтилена высокой плотности. [18]

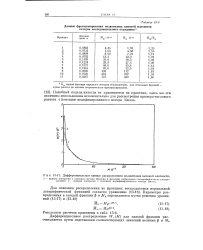Дифференциальные кривые распределения полиэтилена высокой плотности. [19]

Шульца и функции нор-мального логарифмического распределения; 2 - кривая построена с помощью модифицированного метода Билла. [20]

Формулу (7.21) называют универсальным логарифмическим распределением осредненной скорости в пристенной области турбулентного потока. [21]

Для ньютоновских жидкостей известны логарифмическое распределение скоростей, названное также универсальным, поскольку не зависит от критерия Re ( это доказано на основе понятия длина пути смешения, введенного Прандтлем), и степенное распределение. [22]

Допускаемые скорости определены при логарифмическом распределении осредненных скоростей по вертикали. [23]

Уравнение (7.19) выражает так называемое логарифмическое распределение осредненной скорости турбулентного течения в пристенной области. [24]

Этот профиль скорости отличается от логарифмического распределения дополнительным слагаемым, учитывающим изменение интенсивности турбулентности в области смеси. [25]

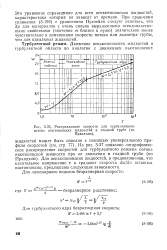Распределение скорости для турбулентного. [26]

На рис. 3 - 37 показано логарифмическое распределение скоростей для турбулентного режима потока ньютоновской жидкости при ее движении в гладкой трубе ( по Прандтлю), Для неньютоновских жидкостей, в предположении, что касательное напряжение т и градиент скорости dw / dn остаются постоянными, предложены следующие зависимости. [27]

В общем виде оно являет собой строго логарифмическое распределение установившегося течения и действительно весьма сильно приближается к нему при подходе к самой скважине. [28]

Используя уравнение для усредненного движения и хорошо установленное логарифмическое распределение скоростей для больших значений у, Васан, Тьен и Уилки [179] нашли полуэмпирические выражения, описывающие непрерывное изменение скорости и турбулентной вязкости в пристеночной области. [29]

Хлопина с сотрудниками было показано, что логарифмическое распределение является частным случаем распределения по закону Хлопина, так как при медленной кристаллизации для каждого отдельного слоя применим вышеуказанный за - он. [30]

Страницы: 1 2 3 4 5