Логарифмическое распределение

Cтраница 4

Изотермическое испарение раствора макрокомпонента в присутствии осадка создает благоприятные условия для логарифмического распределения микрокомпонента. При изотермическом испарении гомогенного раствора происходит постепенное увеличение его пересыщения, скорость возрастания которого зависит от скорости испарения. Если же испарение протекает в присутствии предварительно введенных кристаллов макрокомпонента, то происходит рост кристаллов макрокомпонента. В результате одновременного испарения и роста кристаллов в системе устанавливается постоянное пересыщение, величина которого зависит от массы осадка, перемешивания раствора, способствующего росту кристаллов, и скорости испарения. [46]

Радиус зоны двухфазной фильтрации Ra можно в первом приближении оценить, приняв логарифмическое распределение давления в пласте. [47]

Сравнивая ( 20) с ( 19), убеждаемся, что логарифмическим распределением скоростей ( 17) можно пользоваться приближенно в области значений у, значительно меньших h, но в то же время в некотором удалении от стенки, где влияние вязких членов пренебрежимо. [48]

Другим предельным случаем распределения микрокомпонента по объему кристаллов при сокристаллизации является так называемое логарифмическое распределение. Оно наступает, когда осадок выделяется из слабо пересыщенного раствора путем снятия пересыщения на заранее внесенных затравках. Соблюдение всех этих условий приводит к тому, что в любой момент времени поверхность кристаллов находится в равновесии с жидкой фазой, и в растворе отсутствуют градиенты концентраций. [49]

При возникновении отказов в результате усталостных разрушений и некоторых видов старения часто возникает нормальное логарифмическое распределение. Случайная величина, например, наработка до отказа w, распределена логарифмически, если ее логарифм х распределен нормально. [50]

Время перераспределения давления в пласте в сутках соответствует времени, необходимому для образования логарифмического распределения давления в направлении любого радиуса дренирования ге. [51]

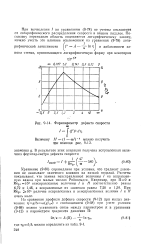Формпараметр дефекта скорости. [52]

При вычислении / по уравнениям ( 9 - 78) не учтены отклонений от логарифмического распределения скорости в вязком подслое. [53]

Эти практические факторы и обусловливают определенное предпочтение другим типам симметричного распределения, в частности удобны однородное, треугольное, косинусоидальное, логарифмическое распределения и распределение Лапласа. Интегралы от этих распределений являются аналитическими функциями. Каждое из первых трех - имеет конечную область существования, последние два - бесконечную. В частности, они могут быть удобны для специальных полей, но значительно менее широко используются по сравнению с нормальным распределением и поэтому в дальнейшем здесь не обсуждаются. Во многих статистических случаях точная природа распределения не важна, но, даже если бы это и требовалось, количество экспериментальных данных настолько ограничено, что точный вид распределения не внесет большей определенности. С другой стороны, нормальное распределение является базисом, для которого уже разработана процедура аппроксимации кривых, а поэтому имеются все возможности для обсуждения испытаний с общих позиций. [54]

Если предположить, что напряжение постоянно и равно TO, интегрирование этого уравнения приводит к логарифмическому распределению скорости. Когда т то ( 1 - У / ГО), получается решение более сложного вида, которое почти так же хорошо соответствует опытным данным, как и решение простого вида. [55]

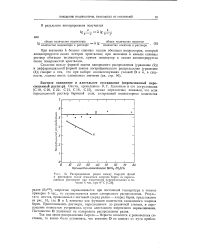Распределение радия между твердой фазой и раствором после осаждения хлорида бария из пересыщенных растворов при энергичном перемешивании в течение 6 час. при 0 С [ С20 ]. [56]

Сходство между формой закона однородного распределения [ уравнение ( 2) ] и дифференциальной формой закона логарифмического распределения [ уравнение ( 4) ] говорит о том, что при выборе соответствующих условий D и X, в сущности, лолжны иметь одинаковые значения ( см. стр. [57]

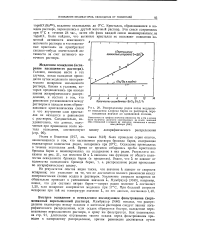Распределение радия после медленного осаждения хлорида бария из растворов, пересыщенных вначале до одинаковой степени. [58]

Мумбрауер [ М40 ] показал, что распределение индикатора между осадком и маточным раствором следует закону логарифмического распределения, если осадок образуется быстро, вследствие перемешивания пересыщенного раствора, и сразу же фильтруется. [59]

Отметим, что согласно экспериментальным данным ( рис. 11.5) переход из вязкого подслоя в зону логарифмического распределения скорости происходит, по-видимому, непрерывно без скачка производной dwjdz на границе вязкого подслоя. Это означает, что резкой границы между вязким подслоем и зоной, где скорость распределена по логарифмическому закону, нет. [60]

Страницы: 1 2 3 4 5