Смешанное распределение

Cтраница 2

В аналитической работе, так же как и во многих других областях техники, часто приходится иметь дело со смешанными ( неоднородными) распределениями, когда рассматриваемая совокупность образована смешиванием двух или даже нескольких генеральных совокупностей с разными параметрами. При смешивании двух генеральных совокупностей обычно получаются асимметричные распределения, а иногда также двухвершинные кривые или кривые с более пологой вершиной, чем это имеет место для нормального распределения. Форма кривых смешанных распределений определяется, с одной стороны, тем соотношением, в котором смешаны два распределения, а с другой стороны - тем, насколько отличаются параметры смешиваемых генеральных совокупностей. [16]

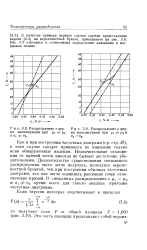Распределение с двумя максимумами при х ( ф Hz и i о 2. [17]

Незначительные отклонения от прямой почти никогда не бывают достаточно убедительными. Доказательство существования смешанного распределения часто легче получить, пользуясь вероятностной бумагой, чем при построении обычных частотных диаграмм, так как легче оценивать рассеяние точек относительно прямой. [18]

Это распределение редко применяется в технике. Оно может иметь место при наложении нескольких распределений Пуассона. Его можно разделить на составляющие путем расчета, или тем же графическим способом, который применяется для нормального смешанного распределения ( см. разд. [19]

Кроме систем с верхней и нижней разводкой, применяют системы со смешанным распределением пара. В этих системах пар в приборы верхних этажей поступает снизу, а в приборы нижних этажей - сверху. Паровую линию в этом случае прокладывают по полу или под потолком одного из этажей. Схемы со смешанным распределением могут быть выполнены как с сухим, так и с мокрым конденсатопроводом. [20]

Зависимость отношения ( г среднего заряда в октаэдрических и тетраэдрических центрах в обратной структуре шпинели ММ О4 от числа адсорбируемых атомов кислорода. [21]

Преимущественным распределением в адсорбционном слое, по-видимому, должно быть то, которое позволяет в процессе адсорбции кислорода сохранить катионную структуру обратной шпинели, существовавшую в исходном твердом теле. С целью нахождения характера этого распределения целесообразно рассмотреть изменение отношения г между средними зарядами катионов в А - и В - центрах. Это отношение равно 3 / 2, 5 / и 1 для соответственно нормальной, обратной и полностью смешанной шпинельных структур. Для случая ( а) распределение в адсорбционном слое изменяется от обратной структуры к нормальной. Для случая ( б) оно остается неизменным, а для случая ( в) следует принять смешанное распределение. Распределение вакансий, соответствующее случаю ( б), наиболее вероятно, если адсорбционный слой строится в соответствии с топо-химическими условиями на поверхности идеальной обратной шпинели. [22]

Значения основных параметров простых ферритов со структурой шпинели. [23]

В структуре типа шпинели иоиы кислорода образуют гранецентрированную кубическую решетку с ребром а. В промежутках между ионами кислорода находятся ионы металлов, причем эти ионы окружены четырьмя или шестью ионами кислорода. Такие окружения называют соответственно тетраэдрическими ( или А) и октаэдрическими ( или S) позициями. Шпинели, в которых ионы Ме2 находятся в тетраэдрических позициях, а ионы Fe3 - в октаэдрических, называют нормальными. Если ионы Ме2 и половина ионов Fe3 находятся в октаэдрических позициях, то шпинель называют обращенной. При смешанном распределении двухвалентные ионы металла находятся как в А -, так и в В-позициях. [24]

Примерами концептуального подхода являются модели распределения химического элемента в горных породах, построенные А. Б. Вистелиусом, Д. А. Родионовым и др. С иными подходами к процедуре выбора теоретического распределения вероятностей ( механическая, физическая и другие модели) можно познакомиться в работах Дж. Общим условием использования теоретической плотности распределения для решения указанных выше задач является достаточно хорошая согласованность выбранной плотности распределения с эмпирически наблюдаемым частотным распределением. Следует, однако, помнить, что выборочные данные могут удовлетворять сразу нескольким плотностям распределения вероятностей, в связи с чем принятие того или иного конкретного закона распределения в качестве вероятностной модели изучаемого природного явления почти всегда гипотетично. С другой стороны, имеются определенные трудности в проверке согласованности теоретической плотности распределения, выбранной на основании вневероятностных соображений ( например, при физико-химическом анализе явления), и эмпирического частотного распределения. Дело в том, что выборочные данные, как правило, отягощены различного рода методическими погрешностями. Последние могут существенно искажать исходное распределение. Еще одна сложность связана с возможной статистической неоднородностью исследуемого объекта, что может, как и в предыдущем случае, приводить к появлению смешанных распределений. [25]

Страницы: 1 2