Гиперболическое распределение

Cтраница 1

Гиперболическое распределение, представленное в виде (5.51) - (5.52) называют законом Парето, в честь итальянского экономиста Вильфредо Парето, обнаружившего, что количество людей с доходом, превышающим некоторую величину х, уменьшается с ростом х гиперболически. [1]

Термин асимптотически гиперболическое распределение можно рассматривать как синоним термина, хорошо знакомого статистикам-экономистам, а именно: распределение Парето. [2]

Хп имела асимптотически гиперболическое распределение с показателем D ( см. главу 38); г) необходимое и достаточное условие приводится в источниках, перечисленных в начале этого раздела. [3]

Поскольку относительная площадь демонстрирует гиперболическое распределение с показателем, близким к единице, и поскольку сумма всех относительных площадей равна 1, можно заключить, что величина ( относительная площадь чаши) 1 й 2 весьма мала. Исключения из общего правила возникают тогда, когда наибольшая чаша чрезвычайно велика; такие чаши заполнять необязательно, как это и произошло в случае Большого Соленого озера. [4]

Следует отметить, что гиперболическое распределение запасов становится явно видным только для хорошо разведанных регионов. [5]

Определим, пользуясь законом гиперболического распределения априорной вероятности измеряемой величины, ее исходную энтропию. [6]

Между стержнями создается поле с гиперболическим распределением потенциала. При фиксированных значениях частоты со и амплитуды U переменного поля только ионы с определенным значением m / z проходят через анализатор, попадая на коллектор ионов. [7]

Еще одна знакомая история: из гиперболического распределения следуют прямые условные распределения. [8]

Утверждается, что площади озер также подчиняются гиперболическому распределению, то есть может возникнуть искушение оставить озера в покое, так как ничего нового они нам не поведают. По более зрелом размышлении, однако, можно заметить, что определения озер и океанических островов ни в коем случае не являются симметричными. [9]

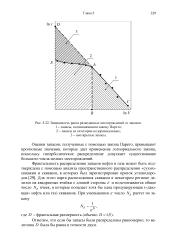Зависимость ранга разведанных месторождений от запасов. [10]

Оценки запасов, полученные с помощью закона Парето, превышают прогнозные значения, которые дает применение логнормального закона, поскольку гиперболическое распределение допускает существование большого числа мелких месторождений. [11]

Таблица показывает, что для сечения тп, которое находится па сравнительно большом расстоянии от точек приложения нагрузки Р, гиперболическое распределение напряжений дает результаты, весьма близкие к точным. [12]

Таблица показывает, что для сечения тп, которое находится на сравнительно большом расстоянии от точек приложения нагрузки Р, гиперболическое распределение напряжений дает результаты, весьма близкие к точным. [13]

Можно отметить, что усредненная величина а01 - - 10 настолько велика, что sh ао / и ch ао / практически бесконечны, и гиперболическое распределение напряжений как при заземленной, так и незаземленной нейтрали приводит напряжения к нулю при расстояниях х от начала обмотки, меньших I. Ход кривых распределения ( [ и ( х) ]) для заземленной и незаземленной нейтралей, особенно в более удаленных точках, весьма сходен. [14]

Этот результат противоречит общепринятому мнению, согласно которому распределение указанных величин следует логарифмически нормальному закону. Различие чрезвычайно значительно, так как при гиперболическом распределении получается гораздо больше ресурсов, чем при логарифмически нормальном. [15]

Страницы: 1 2