Гладкое распределение

Cтраница 1

Гладкое распределение Д на Р является горизонтальным распределением нек-рой линейной С. [1]

Политропами описываются не только системы с гладким распределением массы, они могут выступать и в качестве первого приближения систем, содержащих сингулярность или же имеющих очень компактное ядро. Это ядро может представлять собой массивный объект, газовое облако или же плотное звездное скопление, которое может считаться до известной степени изолированным от остальной части системы. Например, в центре скопления галактик может находиться очень массивная галактика; ядро галактики может содержать массивную черную дыру. [2]

Уточнения нормального приближения в многомерном случае для гладких распределений имеют тот же характер, что и в одномерном случае. [3]

В этом случае необходимо либо аппроксимировать меру гладким распределением, либо решать уравнение Перрона-Фробениуса, либо вообще отказаться от исследований такого рода. [4]

Докажем, что электростатическое поле, созданное гладким распределением зарядов простого слоя на гладкой ограниченной поверхности, ограничено вплоть до границы. [5]

Такая форма существует тогда, когда протяженный хвост гладкого распределения был обрезан и собран в одну единственную категорию на краю диапазона данных. Кроме того, это может указывать на неаккуратную запись данных. [6]

Причина этого упрощения состоит в том, что при гладком распределении скоростей пропадает необходимость учитывать те моды, которые появляются в каждом отдельном односкоростном потоке. Среди всех этих мод есть, в частности, одна, которая не возрастает и не затухает. Она также и не распространяется и вообще существует только в данной области. Это критическая мода со 0, соответствующая порогу джинсовской неустойчивости. [7]

Эта мысль находит себе оправдание в том общеизвестном факте, что для сравнительно гладких распределений внешней скорости уже однопараметрическое приближение можно считать вполне удовлетворительным. [8]

Пример с простой волной сжатия показывает, что даже при сколь угодно гладких распределениях искомых величин в начальных или краевых условиях описанных выше типичных задач I - III их решение может не существовать не только в классе гладких функций, но и в классе непрерывных функций. [9]

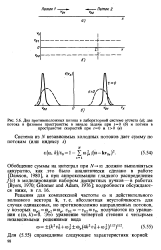Два противоположных потока в лабораторной системе отсчета ( а. два. [10]

Обобщение суммы на интеграл при N - co должно выполняться аккуратно, как это было аналитически сделано в работе [ Dawson, 1980 ], а при аппроксимации гладкого распределения f ( v) в моделировании набором дискретных пучков - в работах [ Byers, 1970; Gitomer and Adam, 1976 ]; подробности обсуждаются ниже, в гл. [11]

Некоторое отличие заключается в распределении температуры внутри зоны реакции: при использовании прямого подхода было взято распределение температуры с изломом ( что, как указано выше, совершенно не обязательно), тогда как стандартная процедура асимптотического метода дает сразу же гладкое распределение. Иное распределение температуры приводит к появлению дополнительных множителей, зависящих от отношения энергий активации Ег1Е %, в выражениях для концентрации активных центров и для массовой скорости горения. [12]

Настоящая статья имеет прямое отношение к теории резонансных состояний и резонансных частот радиального уравнения Шредингера с короткодействующим потенциалом и приводит к некоторым новым результатам в этой теории. При отсутствии связанных состояний соответствующая граничная задача легко преобразуется в задачу ( 1), ( 2) с гладким распределением масс. Мы надеемся в дальнейшем подробнее остановиться на этой связи. [13]

В этом вопросе необходимо стать на практическую точку зрения: если по отношению к данному частному применению закон незаметен, то для данного применения числа случайны, и мы должны этим удовлетвориться. В самом деле, с практической точки зрения, быть может, и не требуется иметь действительно случайную последовательность, а предпочтительнее более гладкое распределение, исчерпывающее часть совокупности без повторений. [14]

Конечно, возмущение х ( 1) не затухает и может нарастать, только его вклад в значение р ( 1) уменьшается при усреднении по гладкому распределению / 0 в осциллирующем поле. [15]

Страницы: 1 2