Рассмотренное распределение

Cтраница 1

Рассмотренное распределение имеет два параметра: аир, но нетрудно убедиться, что вид кривой зависит только от первого из них, второй же играет в нем лишь роль масштаба, в котором представлена распределенная величина. Это видно хотя бы из того, что в вышеприведенной таблице начальных и Центральных моментов параметр р входит везде множителем в степени порядка момента. [1]

Рассмотренное распределение называется жспоненциальным распределением. [2]

Рассмотренное распределение называется экспоненциальным распределением. [3]

Рассмотренное распределение потенциалов в пограничном с жидкостью слое газа может служить основой для построения модели, теоретического анализа и получения расчетных зависимостей процессов тепло - и массообмена. [4]

Рассмотренное распределение температуры наблюдается при течении смазочного масла в щели между цапфой и подшипником и играет здесь важную роль. При малых размерах щели и большой вязкости смазочного масла такое течение получается ламинарным. Тепло, возникающее в смазочном слое вследствие трения, вызывает значительное нагревание даже при умеренных скоростях движения, как это показывает следующий численный пример. Вязкость смазочного масла при умеренной температуре ( примерно при 30 С), согласно таблице 12.1, равна ы 0 4 кг / м сек, коэффициент теплопроводности масла равен К 0 14 дж / м сек град. [5]

Помимо рассмотренного распределения динамического давления, появляющегося благодаря обтеканию цилиндра, одновременно на поверхность последнего действует также динамическое давление, возникающее вследствие возмущения потока, вызываемого державкой. Это давление ( кривая / /), имеющее положительное значение вблизи державки, сильно понижается по мере приближения к концу цилиндра. [6]

Помимо уже рассмотренных распределений теплового потока, ограниченные результаты были получены также для опытных участков с локализованными пиками теплового потока. Степень интенсивности и длина пиков теплового потока систематически изменяли, чтобы можно было исследовать применимость предложенной модели к этому случаю. [7]

С рассмотренными распределениями тесно связано так называемое отрицательно-биномиальное распределение, называемое также распределением Паскаля. Речь идет о вероятности того, что в последовательности испытаний Бернулли для достижения п успехов потребуется n k испытаний. [8]

В рассмотренном распределении потенциала для электрона, эмиттированного катодом, мы не учли один весьма важный факт. Поскольку горб потенциальной кривой ( см. Ъ на рис. 113) находится вне катода, часть электронов, которые имеют скорости, достаточные для вылета из катода, но недостаточные для преодоления потенциального барьера, создадут электронное облако вблизи катода. Отрицательный объемный заряд этого облака повышает потенциальный барьер. [9]

Если применить рассмотренное распределение к отдельным молекулам идеального газа, которые не взаимодействуют одна с другой, то квантово-механическая задача об определении уровней энергии Еп всего газа в целом сводится к задаче определения уровней энергии отдельной молекулы. [10]

Если применить рассмотренное распределение к отдельным молекулам идеального газа, которые не взаимодействуют одна с другой, то квантово-механическая задача об определении уровней энергии Е всего газа в целом сводится к задаче определения уровней энергии отдельной молекулы. [11]

Наряду с рассмотренными распределениями важную роль в дисперсионном анализе играет F-распределение. [12]

Видно, что для всех рассмотренных распределений, кроме №, обрезание концов вариационного ряда значительно повышает эффективность. [13]

В табл. 8.6 дана картина ранее рассмотренного распределения отклонений. [14]

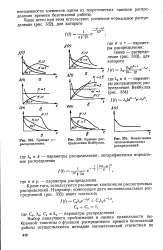Кривые Y - распределения.| Кривые распределения Вейбулла. [15]

Страницы: 1 2