Двумерное распределение

Cтраница 1

Двумерное распределение слабо характеризует статистические зависимости между переменными величинами вакуумной колонны. [1]

Двумерное распределение частот, полученное при определении калия в двух пробах. [2]

Двумерное распределение частот, полученное при определении влажности в двух пробах. [3]

Двумерное распределение пятен определяется спецификой фононной подсистемы ( пространственной стехиометрией ионной решетки) и топологией дислокаций на ней. [4]

Рассмотрим двумерное распределение температуры в цилиндрическом теле произвольного поперечного сечения, считая, что температура остается постоянной вдоль любой прямой линии, параллельной образующей цилиндра. Пусть существует стационарное состояние ( температура не изменяется со временем) и пусть вдоль контура температура распределена произвольным образом. [5]

Зависимость инвариантного сечения кумулятивного процесса рождения протонов ( с импульсом 0 4 - 1 0 ГэВ / с в интервале углов 160 - Ifi4 на разных ядрах от энергии. налетающих пионов и протонов ( зачерненный точки. j n.| Зависимость от х инвариантного сечения кумулятивного процесса при пулевом поперечном импульсе рт кумулятивной частицы. Точки, крестики и квадратики относится соответственно к я - мсзонам, К - мезонам и К - - мезонам. [6]

Для двумерного распределения Гаусса отличны от 0 только К. [7]

Функция исходного двумерного распределения ср0 ( /, р0) считается известной. Построив функцию fn ( gn, р), мы тем самым находим распределение вероятностей значений пропускной способности при любом фиксированном значении рп. [8]

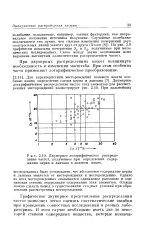Двумерное логарифмическое распределение частот, полученное при определении содержания церия и лантана в полевом шпате. [9]

При двумерных распределениях может возникнуть необходимость в изменении масштаба. При этом особенно часто применяют логарифмическое преобразование. [10]

Проектированием массы двумерного распределения на одну из координатных осей получим ( см. параграф 8.4) частное распределение соответствующей величины. [11]

В случае двумерного распределения мы видели, что величина (29.8.4), связанная простым образом с выборочным коэффициентом регрессии, имеет - распределение ел - 2 степенями свободы. Этот результат был обобщен Бартлетом [54] на случай распределений любого числа измерений. [12]

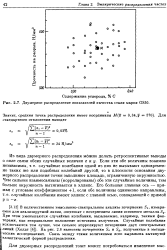Двумерное распределение показателей качества стали марки GS50. [13]

Из вида двумерного распределения мбжно делать ретроспективные выводы о силе связи обеих случайных величин х и у. Чем сильнее взаимосвязаны ( коррелированы) обе эти случайные величины, тем больше окружность вытягивается в эллипс. [14]

Статистическими методами двумерных распределений также нельзя было в достаточной мере однозначно доказать правильность теории склонности к авариям. В соответствии с двумерным анализом распределений лица с высокой склонностью к авариям при тех же условиях в будущем должны снова допускать аварии, в то время как лица с низкой склонностью и в дальнейшем не должны допускать аварий. [15]

Страницы: 1 2 3 4 5