Двумерное распределение

Cтраница 3

Метод хода лучей основан на построении двумерного распределения интенсивности в фокальной плоскости системы с помощью дискретных лучей, траектории которых определяются их координатами и направляющими косинусами на входном отверстии системы, а также геометрией поверхностей зеркал. При существующей точности изготовления искажения фронта волны при отражении значительно больше дифракционных пределов, поэтому фазовые соотношения между отдельными лучами в фокальной плоскости не учитываются. Таким образом, расчет по методу хода лучей ведется в рамках геометрической оптики. Важным обстоятельством для рентгеновской области спектра является то, что расчет траектории каждого луча позволяет определить точные значения локальных углов скольжения на каждом из зеркал, от которых зависят и коэффициенты отражения. [31]

Этот результат был получен пересчетом по двумерному распределению давления на плоской пластине относительно оси симметрии. Однако при / С 1 3 более простая линейная формула (5.10) дает не менее точные результаты. [32]

Предположим, что Xi и Xz имеют двустороннее двумерное распределение Парето с параметрами г4, г2 и а. [33]

Очевидно, по указанной статистике однозначно восстанавливается двумерное распределение случайного вектора ( а, Р), где а - интервал между окончанием обслуживания - го и ( п 1) - го требований, р - то же для ( п 1) - го и ( п 2) - го требований. [34]

Фотографическое изображение, или фотограмма, представляет собой двумерное распределение оптической плотности, которому соответствует геометрическое распределение количества света, воздействовавшего на фотослой. [35]

На практике в подавляющем большинстве случаев используются только одномерные и двумерные распределения. [36]

Это и доказывает утверждение о возможности восстановления двумерного распределения по одномерным для независимых случайных величин: нужно просто перемножить их функции или плотности распределения. [37]

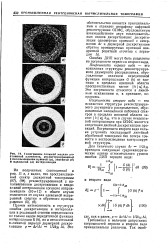Томограммы сложной модели постоянной плотности, реконструированные с использованием нулевой ( а, линейной ( о И идеальной ( в интерполяции. [38]

Погрешности второго вида - это искажения структуры реконструируемого двумерного распределения, обусловленные наложением побочных спектров в пределах основной области частот k; Нм, что в случае неидеальной интерполяции при ОПФС является следствием двойной дискретизации проекций. [39]

Кроме них необходимо еще иметь в своем распоряжении двумерное распределение вероятностей. [40]

Если плотность р ( х, у) двумерного распределения задана, то можно определить одномерные функции распределения и плотности. [41]

Покажем, что выражение (5.2.38) действительно является плотностью двумерного распределения двух линейно коррелированных величин X и Y, каждая из которых в отдельности нормально распределена с соответствующими значениями центра и дисперсии. В одном частном случае это обстоятельство делается очевидным. [42]

Полярная ( а и декартова ( б сетки отсчетов. [43]

Источник-Детектор на угол, является сечением двумерного фурье-образа искомого двумерного распределения по линии, проходящей через начало координат ( центральным сечением) и повернутой на угол &. Таким образом, из одномерных фурье-образов проекций можно набрать ( синтезировать) двумерный фурье-образ искомого изображения, которое затем можно восстановить с помощью двумерного обратного преобразования Фурье. [44]

После преобразования координат дальнейшие операции по представлению функций плотности двумерных распределений рядами мало отличаются от одномерного случая. [45]

Страницы: 1 2 3 4 5