Регулярное распределение

Cтраница 2

Это создает представление о теплообмене в области регулярных распределений как о явлении чистой теплопроводности. Такое понимание природы теплообмена находится в полном согласии с общими представлениями о механизме переноса теплоты в ламинарно движущейся жидкости, так как в этих условиях явления обмена должны рассматриваться как эффекты молекулярной природы. [16]

Для создания гибких и эластичных структур с регулярным распределением в каркасе полимера ионогенных групп, а также для улучшения кинетических и сорбционных свойств ионитов целесообразно осуществлять их синтез из мономеров и олигоме-ров, уже содержащих электронодонорные функциональные группы, путем сополимеризации или поликонденсации с соответствующим подбором сшивающих агентов. [17]

Тем не менее б безусловно не является регулярным распределением. [18]

Регулярное расположение неупорядоченных областей по всей. [19]

Наиболее очевидным недостатком приведенной модели является предположение о регулярном распределении неупорядоченных областей. В действительности такие области могут появляться в любых произвольных точках по всему объему кристалла. По-видимому, можно, однако, считать, что в условиях равновесия при данной температуре все неупорядоченные области имеют одинаковый размер, но их первоначальное распределение существенно для определения момента, когда все эти неупорядоченные области начинают сливаться. [20]

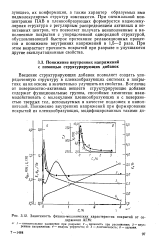Зависимость физико-механических характеристик покрытий от содержания АГМ. [21]

При оптимальной концентрации ПАВ в пленкообразующих формируется надмолекулярная структура с регулярным распределением активных и неактивных центров, что позволяет получать ненаполненные и наполненные покрытия с упорядоченной однородной структурой, обусловливающей быстрое протекание релаксационных процессов и понижение внутренних напряжений в 1 5 - 2 раза. При этом возрастает прочность покрытий при разрыве и улучшаются другие эксплуатационные свойства. [22]

Изменение электросопротивления R ( 1 - 3 и влажности U ( Я - З1 при формировании пленок из различных. [23]

В дисперсиях на основе полиалкилакри-латов с высокой концентрацией полярных групп [56] или регулярным распределением их в цепи в случае полиуретановых систем [30] частицы состоят из плотно упакованных развернутых макромолекул. Структура таких частиц не выявляется при длительном кислородном травлении и диспергировании с помощью ультразвука. [24]

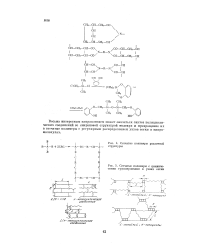Сетчатые полимеры различной структуры.| Сетчатые полимеры с циклическими группировками в узлах сетки. [25]

Весьма интересным направлением может оказаться синтез полициклических соединений со спирановой структурой молекул и превращение их в сетчатые полимеры с регулярным распределением узлов сетки в макромолекулах. [26]

Можно ожидать, что крутильные деформационные колебания СН2, поскольку они, как и маятниковые колебания СН2, являются внеплоскостными, будут давать регулярное распределение полос. [27]

Глюкозидные связи, расположенные у концов цепей, по-видимому, аиболее чувствительны к гидролизу, но некоторые авторы полагают, что разрыв цепей облегчается благодаря регулярному распределению наиболее реакционноспособных групп. [28]

Кнезер) поставил себе еще более широкую задачу, содержащую исследование кривых, удовлетворяющих на торе дифференциальному уравнению ( 1), как частный случай, а именно - исследовать регулярное распределение кривых на поверхностях двухстороннего и одностороннего тора. Если в работе Кне-зера ограничиться тем, что относится к кривым на двухстороннем ( обычном) торе, то задача ставится так: исследовать регулярные семейства кривых на торе. Под регулярным, на поверхности F, семейством кривых понимают семейство кривых, обладающих следующим свойством: через каждую точку Я поверхности F проходит единственная кривая, при этом для любой точки Р существует окрестность, которую можно так отобразить на квадрат, что кривые семейства перейдут в семейство прямых, параллельных стороне квадрата. [29]

Следует отметить, что решение уравнений для компонент напряжений, деформаций и перемещений может быть найдено в аналитической форме лишь для тел несложной геометрической формы при упрощенных граничных условиях и регулярном распределении температуры. Именно такие условия часто реализуются в лазерной технике. Обычный для лазерных элементов характер температурного распределения ( зависимость Т лишь от одной координаты) позволяет существенно упростить решение задачи термоупругости, введя приближения плоскодеформированного или плосконапряженного состояния. [30]

Страницы: 1 2 3 4