Практическое кривое распределение

Cтраница 2

Время от времени должны обязательно делаться сводки результатов последующего контроля готовой продукции ( сплошного и выборочного) и текущего контроля по контрольным диаграммам в виде: а) построения практических кривых распределения и сопоставления их с теоретическими ( методами, указанными на стр. [16]

Экспериментальные исследования показали, что при существующих условиях обработки на агрегатно-расточных станках с ручной подачей точность продольных размеров деталей определяется 4 - 5 классами. Соответствующие практические кривые распределения приведены на фиг. [17]

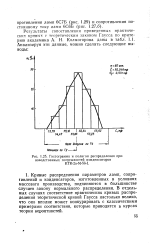Гистограмма и полигон распределения производственных погрешностей конденсаторов KTK-23 - M-56-I. [18]

Кривые распределения параметров ламп, сопротивлений и конденсаторов, изготовленных в условиях массового производства, подчиняются в большинстве случаев закону нормального распределения. В отдельных случаях соответствие практических кривых распределения теоретической кривой Гаусса настолько велико, что оно вполне может конкурировать с классическими примерами соответствия, которые приводятся в курсах теории вероятностей. [19]

Однако вывести какие-либо закономерности, которые бы давали аналитические зависимости для расчета возможного поля рассеивания размеров ( погрешностей) деталей, на основании анализа данных кривых не представляется возможным. Поэтому при расчетах точности обработки практические кривые распределения заменяются теоретическими кривыми распределения, у которых закон распределения случайных величин определяется соответствующими уравнениями. [20]

Так чаще всего поступают при построении практических кривых распределения. [21]

Практическое поле рассеивания суммарной погрешности обработки ( Ал /) определено на основании суммирования практических кривых распределения по максимальным и минимальным размерам. [22]

Исследование кривых распределения, построенных по результатам обработки партии деталей и основных параметров этого распределения, является распространенным методом анализа точности технологического процесса. Этот метод, подробно разработанный Н. А. Бородачевым, А. Б. Яхиным и др., позволяет количественно характеризовать влияние того или иного фактора на результативную точность технологического процесса в виде изменений формы или положения кривой распределения, вызываемых изменением первичных факторов. Так как практические кривые распределения оказываются ломаными и прерывистыми, то для целей статистического анализа их заменяют соответствующими теоретическими кривыми распределения, отвечающими вполне определенным законам распределения теории вероятностей. [23]

Если расчет точности должен быть выполнен для изготовляемых приборов или аналогичных приборов, уже находящихся в производстве, то отбирают часть деталей, попадающих на сборку приборов, и их тщательно измеряют. На основании числовых результатов измерения могут быть найдены известными способами практические кривые распределения отклонений, а по ним выбраны теоретические кривые распределения, согласующиеся с практическими данными. [24]

На практике имеют место разнообразные виды распределений случайных погрешностей. Нахождение основных характеристик для каждой полученной кривой распределения сильно усложнило бы решение практических задач, связанных с вероятностными расчетами. Советскими учеными ( Н. А. Бородачевым и др.) разработаны основные типы законов распределения производственных, случайных погрешностей. Это дало возможность относить практические кривые распределения к близким теоретическим кривым, для которых характеристики рассеивания уже установлены. [25]

На практике имеют место разнообразные виды распределений случайных погрешностей. Нахождение основных характеристик для каждой полученной кривой распределения сильно усложнило бы решение практических задач, связанных с вероятностными расчетами. Советскими учеными ( Н. А. Бородачевым и др.) разработаны основные типы законов распределения производственных случайных погрешностей. Это дало возможность относить практические кривые распределения к близким теоретическим кривым, для которых характеристики рассеивания уже установлены. [26]

Симпсона ( распределение по треугольнику, фиг. Закон Гаусса относится к последней группе законов распределения. Рассматриваются также и несимметричные кривые распределения ( фиг. Многочисленные наблюдения и опыты показали, что построенные на основании статистических данных практические кривые распределения близки к кривой Гаусса. [27]

Страницы: 1 2