Теоретическое кривое распределение

Cтраница 1

Теоретические кривые распределения изображают вполне определенные законы распределения случайных величин, заданных некоторыми уравнениями. Эти кривые используются для приближенного выражения действительных законов распределения. [1]

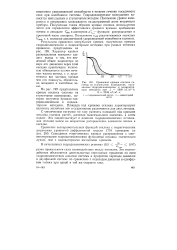Сравнение кривых отклика системы на ступенчатое возмущение, полученных гидродинамическим и индикатор. [2]

Совпадение теоретических кривых распределения с соответствующими гидродинамическими функциями отклика значительно лучше, чем с индикаторными выходными кривыми. [3]

Анализ эмпирических и теоретических кривых распределения вероятностей появления отказов за заданный интервал времени подтверждает, что вероятность появления отказов подчиняется закону Пуассона. [4]

Даже и теоретические кривые распределения здесь будут оправдываться на практике только при условии, что рабочий, изготовляющий детали, действительно следует той самой схеме пробных промеров и ввода ступеней изменения размеров, которые положены в основу теоретических схем. В противном случае на практике будут получаться распределения, представляющие собой произвольные композиции соответственных теоретических схем. [5]

Путем сравнения экспериментальных и теоретических кривых распределения концентраций было установлено, что процесс продольного перемешивания при наложении пульсаций в барботажной - колонне соответствует диффузионной модели. [6]

Сравнение эмпирической и теоретических кривых распределения с помощью критерия Колмогорова [ Р ( К) - 0 81 ] позволяет принять для описания эмпирического распределения нормальный закон. [7]

В математической статистике известно много различных теоретических кривых распределения. [8]

На рис. 25 показаны некоторые теоретические кривые распределения молекулярных весов. [9]

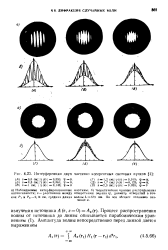Интерференция двух частично когерентных световых пучков. [10]

Наблюдаемые интерференционные картины; б) теоретические кривые распределения интенсивности; s - расстояние между отверстиями экрана Q, диаметр отверстий в точках PI и Р, - 0 14 см, средняя длина волны А. [11]

Равновероятное распре - гДе Р - Вероятность успеха В КЗЖДОМ. [12]

В качестве математических моделей статистических распределений используются теоретические кривые распределения. Теоретическая кривая - это зависимость, которая описывается математически, т.е. может быть выражена уравнением с определенными параметрами. Известно очень много различных распределений, а число потенциально возможных статистических моделей еще больше. Однако на практике используются лишь некоторые из них, обычно те, которые более удобны для описания какой-либо ситуации или обладают желательными математическими свойствами. [13]

По результатам измерений могут быть найдены практические кривые распределения отклонений, а по ним - теоретические кривые распределения, согласующиеся с практическими данными. [14]

Имеется и другой прием построения безусловных функций распределения вероятностей, основанный на использовании так называемых теоретических кривых распределения. [15]

Страницы: 1 2